Ричард Фейнман - Том 3. Квантовая механика

Пусть речь идет об одномерном случае движения электрона, когда потенциальная энергия меняется по х так, как показано на фиг. 14.3.

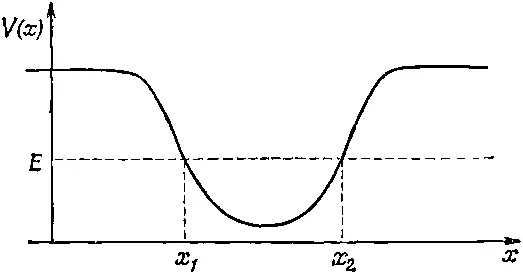
Фиг. 14.3. Потенциальная яма для частицы, движущейся вдоль оси х.

Предположим, что потенциал является статическим: со временем он не меняется. Как уже мы делали много раз, поищем решения, отвечающие состояниям определенной энергии, т. е. определенной частоты. Испытаем такую форму решения:

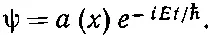(14.57)

Если мы эту функцию подставим в уравнение Шредингера, то увидим, что функция а ( х ) обязана подчиняться следующему дифференциальному уравнению:

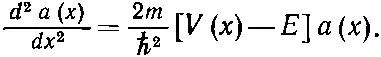(14.58)

Это уравнение говорит, что, каково бы ни было х , вторая производная а ( х ) по х пропорциональна а( х ) с коэффициентом пропорциональности V - Е . Вторая производная от а ( х ) это скорость изменения наклона а ( х ). Если потенциал V больше энергии Е частицы, то скорость изменения наклона а ( х ) будет иметь тот же знак, что и a ( х ). Это значит, что кривая а ( х ) повернута выпуклостью к оси х , т. е. более или менее следует ходу положительной или отрицательной экспоненты е ±x. Это означает, что на участке слева от х 1(см. фиг. 14.3), где V больше предполагаемой энергии Е , функция а ( х ) будет напоминать одну из кривых на фиг. 14.4, а .

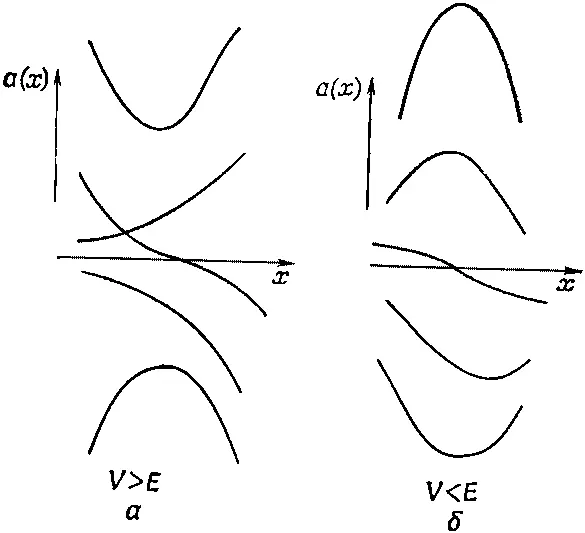
Фиг. 14.4. Возможные формы волновой функции а(х) при V>E и при V

Если же потенциальная функция V меньше энергии Е , то знак второй производной а ( х ) по х противоположен знаку самой а ( х ) и кривая a ( х ) будет всегда вогнута к оси х , подобно одной из линий на фиг. 14.4, б . Решение на этом участке приобретет форму кусочков синусоид.

Теперь поглядим, можем ли мы графически построить решение для функции а ( х ), отвечающей частице с энергией Е а при потенциале V , показанном на фиг. 14.5. Раз нас интересует такое положение, когда частица заключена внутри потенциальной ямы, то мы будем искать решения, при которых амплитуда волны принимает после удаления х за пределы потенциальной ямы очень малые значения. Мы очень легко можем представить себе кривую наподобие изображенной на фиг. 14.5, стремящуюся к нулю при больших отрицательных х и плавно поднимающуюся при приближении к х 1. Поскольку V в точке х 1равно Е а , то кривизна функции в этой точке равна нулю. Между х 1и х 2величина V - Е а всегда отрицательна, так что функция а ( х ) все время вогнута к оси, а кривизна тем больше, чем больше разность между Е а и V . Если продолжить кривую в область между x 1и x 2, ей придется идти примерно так, как на фиг. 14.5.

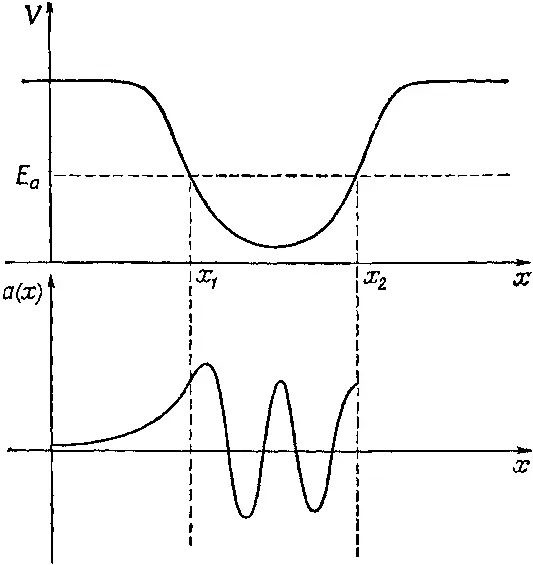
Фиг. 14.5. Волновая функция для энергии Е а , стремящаяся к нулю при удалении х в отрицательную сторону.

Теперь протянем эту кривую правее х 2. Там она искривляется прочь от оси и движется к большим положительным значениям (фиг. 14.6).

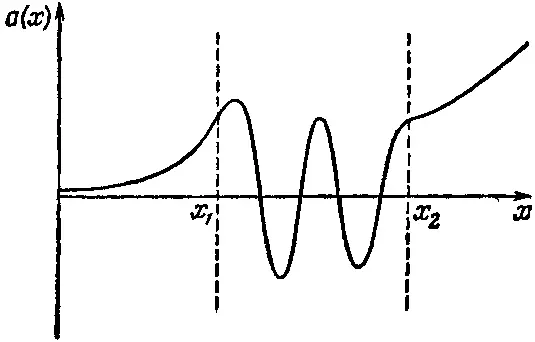
Фиг. 14.6. Волновая функция а(х) (см. фиг. 14.5), продолженная за x 2 .

Для выбранной нами энергии Е а решение a ( х ) с ростом х растет все сильнее и сильнее. Действительно, ведь и кривизна решения а ( х ) тоже возрастает (если потенциал остается почти постоянным). Амплитуда круто вырастает до гигантских масштабов. Что это означает? Просто что частица не «связана» потенциальной ямой. Обнаружить ее вне ямы бесконечно более вероятно, чем внутри . Для изготовленного нами решения гораздо более вероятно встретить электрон в x =+∞, чем где-либо еще. Найти решение для связанной частицы нам не удалось.

Что ж, попробуем взять другую энергию, скажем, чуточку повыше чем Е а , например Е b (фиг. 14.7).

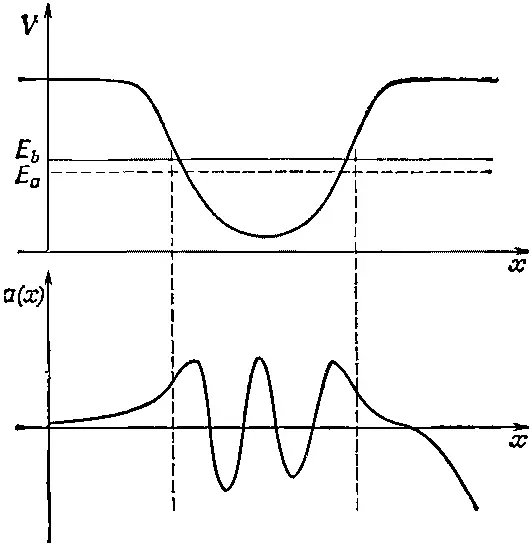
фиг. 14.7. Волновая функция а(х) для энергии e b , большей чем Е а .

Если слева условия останутся теми же, то мы придем к решению, показанному на нижней части фиг. 14.7. На первых порах оно выглядит получше, но в конце концов оказывается таким же плохим, как и решение для Е а , только теперь при возрастании x величина а ( х ) становится все более и более отрицательной .

Может быть, в этом разгадка! Раз небольшое изменение энергии от Е а к Е b приводит к тому, что кривая перебрасывается с одной стороны оси на другую, то, может быть, существует энергия, лежащая между Е а и Е b , при которой кривая для больших х будет стремиться к нулю. Так оно и есть, и мы на фиг. 14.8 изобразили, как может выглядеть решение.

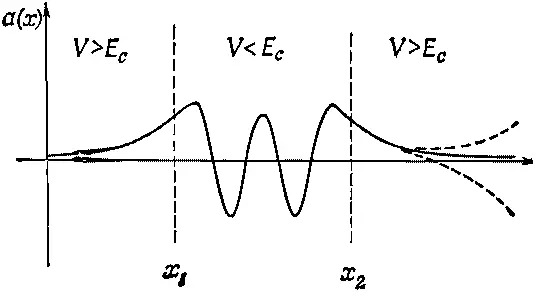
Фиг. 14.8. Волновая функция для энергии Е c между Е а и Е b .

Вам нужно понимать, что решение, показанное на рисунке, это весьма частное решение. Если бы мы даже чуть-чуть подняли или снизили энергию, то функция перешла бы в другие кривые, похожие на одну из штриховых кривых фиг. 14.8, и опять для связанной частицы не получилось бы надлежащих условий. Мы пришли к выводу, что если частица должна находиться в потенциальной яме, то это может с ней случиться только при вполне определенной энергии.

Значит ли это, что у частицы, находящейся в связанном состоянии в потенциальной яме, может быть только одна энергия? Отнюдь. Могут быть и другие, но не слишком близко к Е с . Обратите внимание, что волновая функция на фиг. 14.8 четыре раза пересекает ось на участке х 1 х 2. Если бы мы выбрали энергию значительно ниже Е с , то могло бы получиться решение, которое бы пересекло ось только трижды, только дважды, только единожды или ни разу. Возможные решения намечены на фиг. 14.9.