Ричард Фейнман - Том 3. Квантовая механика

где n — целое число. Иными словами, ток достигает своего максимума, когда зацепляющийся за схему поток принимает те самые квантованные значения, которые мы получили в уравнении (19.30)!

Ток Джозефсона через двойной переход недавно был измерен [103] Jaklevic, Lambe, Silver, Mercereau, Phys. Rev. Letters, 12, 159 (1964). как функция магнитного поля в области между ветвями. Результаты приведены на фиг. 19.8.

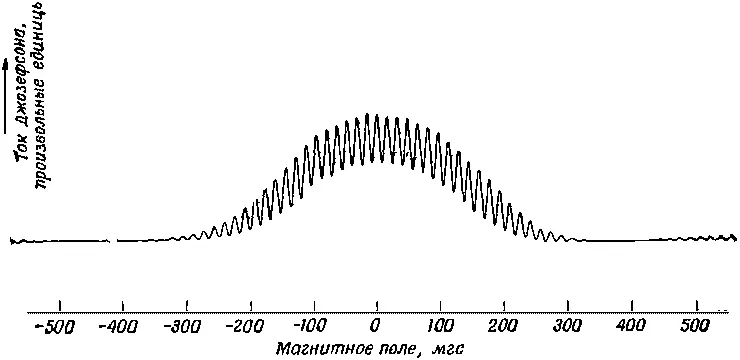
Фиг. 19.8. Запись тока через два параллельных перехода Джозефсона как функции магнитного поля в области между двумя переходами.

Здесь мы видим общий фон от токов, вызываемых различными эффектами, которыми мы пренебрегли, но быстрые колебания тока при изменении магнитного поля объясняются наличием интерференционного члена cos ( q e Ф / ℏ ) в (19.52).

Один из самых интригующих вопросов квантовой механики— это вопрос о том, существует ли векторный потенциал в том месте, где нет поля [104] Jaklevic, Lambe, Silver, Mercereau, Phys. Rev. Letters, 12, 274 (1964). . Опыт, который я только что описал, был проделан тоже с узеньким соленоидом, помещенным между двумя переходами, так что заметное магнитное поле Вбыло только внутри соленоида, а на сверхпроводящие провода его попадало пренебрежимо мало. И вот оказалось, что сила тока колеблется с изменением потока магнитного поля внутри этого соленоида, даже если само поле и не касается проводов. Это еще одно доказательство «физической реальности» векторного потенциала [см. гл. 15, § 5 (вып. 6)].

Я не знаю, что теперь на очереди. Но посмотрите-ка, что можно было бы сделать. Во-первых, заметьте, что интерференция между двумя переходами может быть применена для создания чувствительного магнитометра. Если площадь, охватываемая двумя переходами, равна, скажем, 1 мм 2, то максимумы на кривой фиг. 19.8 будут отстоять друг от друга на 2·10 -5 гс . Одну десятую промежутка между пиками запросто можно заметить; значит, таким соединением можно будет измерять поля величиной в 2·10 -6 гс , или замерять большие поля со столь же хорошей точностью. Можно даже пойти дальше. Представим, например, что мы вплотную друг к другу на равных расстояниях расставили 10—20 переходов. Тогда получится интерференция на 10—20 щелях, и при изменении магнитного поля мы получим очень резкие максимумы и минимумы. Вместо интерференции на двух щелях у нас будет двадцати-, а может быть, и стощелевой интерферометр для измерения магнитного поля. Вероятно, можно предсказать, что измерения магнитных полей при использовании квантовомеханической интерференции станут почти такими же точными, как измерения длин световых волн.

Это еще одна иллюстрация к тому, что происходит в физике в последнее время — появление транзистора, лазера, а теперь эти переходы сверхпроводников, практическое значение которых пока еще не раскрыто полностью. Квантовая механика, открытая в 1926 г., имела за своими плечами почти 40 лет развития, когда вдруг внезапно она получила множество реальных практических применений. Как-то сразу появилась возможность крайне деликатно и тонко управлять природой.

И должен вам сообщить, джентльмены, как это ни прискорбно, что для того, чтобы принять в этом участие, вам абсолютно необходимо как можно быстрее изучить квантовую механику. В этом курсе мы попытались отыскать путь, на котором тайны этой области физики стали бы вам понятными как можно раньше.

Ну что ж, я выступал перед вами два года, пора и перестать. Кое в чем я хотел бы попросить прощения, кое в чем нет. Я надеюсь (более того, знаю!), что человек двадцать-тридцать из вас оказались в состоянии следить за всем с большим подъемом и получили большое удовольствие. Но я знаю и то, что «обучение редко приносит плоды кому-либо, кроме тех, кто предрасположен к нему, но им оно почти не нужно». Значит, о тех двух-трех десятках из вас, которые все понимали, я могу сказать, что лишь раскрыл перед ними истинное положение вещей. Что же касается прочих, то было бы жаль, если бы мои лекции заставили их возненавидеть предмет. Я никогда прежде не преподавал элементарной физики и поэтому приношу им всяческие извинения. Но все же я надеюсь, что не очень вас напугал и вы не бросите этого замечательного занятия. Может быть, кто-нибудь другой выучит вас всему, чему нужно, не вызывая раздражения, и в конце концов вы вдруг поймете, что все это не так страшно, как сперва казалось.

Смею заметить, наконец, что я не ставил себе целью подготовить вас к каким-то экзаменам и даже к работе в промышленности или в военном деле. Я хотел, чтобы большинство из вас смогло оценить красоту нашего прекрасного мира и вместе с тем получить физическое представление о мире, которое, я думаю, составляет сейчас главную часть истинной культуры нашей эпохи. (Вероятно, найдутся преподаватели других дисциплин, которые захотят что-то возразить, но я-то знаю, что они абсолютно неправы.)

А может быть, вы не только сумеете отдать должное этой культуре; не исключено, что и вас самих потянет подключиться к этому величайшему дерзанию, на которое когда-либо пускался человеческий разум.

В американском издании этот том начинается с двух глав из второго тома [гл. 37 и 38 (вып. 3)], которые авторы считали нужным повторить. Это было сделано для того, чтобы третий том можно было читать, не обращаясь к прежним томам. В русском издании мы не стали печатать их снова: читатель должен всегда держать первые выпуски под рукой, поэтому нумерация глав в русском издании сдвинута на 2 единицы по сравнению с третьим томом. Из тех же соображений мы не перепечатали вновь гл. 34 и 35, они вошли в вып. 7.— Прим. ред.

По-русски, наверно, правильнее говорить амплитуда вероятности , но короче говорить просто амплитуда и примириться с выражением типа « амплитуда того, что электрон находится в точке х ».— Прим. ред.

Вообще-то направление рассеяния должно, конечно, описываться двумя углами — полярным углом φ и азимутом θ. Тогда следовало бы сказать, что рассеяние кислорода в направлении (θ,φ) означает, что α-частица движется в направлении (π-θ, φ+π). Однако для кулоновского рассеяния (и многих других случаев) амплитуда рассеяния не зависит от φ. Тогда амплитуда того, что кислород полетел под углом θ, совпадает с амплитудой того, что α-частица полетела под углом (π-θ).

Перестановка dS 1и dS 2в (2.11) приводит к другому событию, так что оба элемента поверхности обязаны пройтись по всей площади счетчика. В (2.13) мы рассматриваем dS 1и dS 2как пару и включаем все, что может случиться. Если интегралы опять включают все, что случится, когда dS 1и dS 2поменяются местами, то все считается дважды.