Ричард Фейнман - Том 3. Квантовая механика

Мы сознаем, что материал этого параграфа длиннее и труднее, чем это положено на нашем уровне знаний. Лучше пропустите его и переходите прямо к § 6. Но если у вас есть самолюбие и время, попозже вернитесь к нему опять. Это великолепнейший пример (взятый к тому же из последних работ по физике высоких энергий) того, что можно сотворить с помощью нашей формулировки квантовой механики двухуровневых систем. (Для русского издания параграф переделан проф. Сэндсом. — Прим. ред.)

Читайте: «.K-нуль с чертой».

Среди новых частиц есть барион Ω -со странностью -3.—Прим. ред.

Если, конечно, он не создает еще двух К +или других частиц с общей странностью +2. Можно считать, что здесь речь идет о реакциях, в которых не хватает энергии для возникновения этих добавочных странных частиц.

Свободная Λ-частица медленно распадается путем слабого взаимодействия (так что странность не обязана при этом сохраняться). Продуктами распада могут быть либо р и π -, либо n и π 0. Время жизни 2,2·10 -10сек.

Типичное время для сильного взаимодействия ближе к 10 -23сек.

Мы здесь упрощаем. Система 2π может иметь множество состояний, отвечающих различным импульсам π-мезонов, и в правой части этого равенства следовало бы поставить сумму по всем базисным состояниям π-мезонов. Но полный вывод все равно приводит к тем же результатам.

Такую интерференцию действительно наблюдали. Коэффициент α оказался равным — 0,96β. Отсюда можно было вычислить и разность масс К 1- и K 2-мезонов. Она оказалась равной около —0,35·10 -5эв. Это наименьшая разность масс двух частиц, известных физикам.— Прим. ред.

Для этих операторов, правда, оказывается, что от их порядка ничего не зависит.

Этот оператор сейчас называют оператор обмена спинами.

В действительности состоянием является

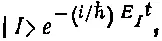
но, как обычно, мы отождествим состояния с постоянными векторами, которые при t=0 совпадают с настоящими векторами.

Crampton, Kleppner, Ramsey, Physical Review Letters, 11, 338 (1963).

Вспомните, что классически U=- μ· B, так что энергия наименьшая, когда момент направлен по полю. Для положительно заряженных частиц магнитный момент параллелен спину, для отрицательных — наоборот. Значит, в (10.27) μ р— число положительное, а μ е— отрицательное.

Тем, кто перескочил через гл. 4, придется пропустить и этот параграф.

Только не старайтесь сделать пакет чересчур узким.

Знак корня, который здесь следовало поставить, это технический вопрос, связанный с допустимыми знаками к в (11.39) и (11.40). Мы не будем здесь вдаваться в подробности.

Литература: Ч. Киттель, Введение в физику твердого тела, М.—Л., 1958, гл. 13, 14, 18.

Во многих книжках эта же энергетическая диаграмма истолковывается иначе. Шкалу энергий относят только к электронам . Вместо того чтобы думать об энергии дырки, говорят о той энергии, которую имел бы электрон, если бы он заполнил дырку. Эта энергия меньше , нежели энергия свободного электрона, причем как раз на ту величину, которая показана на фиг. 12.5. При такой интерпретации шкалы энергий ширина энергетической щели — это наименьшая энергия, которой нужно снабдить электрон , чтобы перевести его из связанного состояния в зону проводимости.

Основное состояние здесь на самом деле «вырождено». Существуют и другие состояния с той же энергией, например, когда все спины смотрят вниз или в любую другую сторону. Но наложение самого слабого внешнего поля в направлении z снабдит все эти состояния различной энергией, и истинным основным состоянием окажется как раз то, которое мы выбрали.

Квазичастицы обсуждаемого типа могут действовать и как бозе- и как ферми-частицы; и, как и у свободных частиц, частицы с целым спином суть бозоны, с полуцелым—фермионы. «Магнон» символизирует, что электрон со спином, направленным вверх, перевертывается вниз. Спин меняется на единицу. Значит, у магнона спин целый и он — бозон.

Могло бы показаться, что при четном N есть N+1 состояний. Это не так, ибо s=±N/2 дают одно и то же состояние.

Когда имеется пара состояний (с разными распределениями амплитуд) с той же энергией, мы говорим, что эта пара состояний «вырождена». Заметьте, что энергией E 0-А могут обладать четыре электрона.

Отношение сторон прямоугольника, который можно разбить на квадрат и на подобный ему прямоугольник.

Представьте себе, что по мере сближения точек х nамплитуда А прыжков из х n=1в х nвозрастает.

О распределениях вероятностей шла речь в гл. 6, § 4 (вып. 1).

Был использован тот факт, что -∞∫ +∞ exp (- t 2) dt =√π; см. вып. 1

Помните, еще раньше мы условились, что e 2≡ q e 2/4πε 0

Литература: А. Р. Эдмондс, Угловые моменты в квантовой механике, в кн. «Деформация атомных ядер», ИЛ, 1958.

Кстати, вы можете доказать, что ^ Q — это обязательно унитарный оператор , т. е. если он действует на |ψ>, приводя к |ψ>, умноженному на некоторое число, то это число должно иметь вид е iδ, где δ — вещественно. Это мелкое замечание, а доказательство основано на следующем наблюдении. Всякая операция наподобие отражения или поворота не приводит к потере каких-либо частиц, так что нормировки |ψ'> и |ψ> должны совпадать; отличаться они вправе только на множитель с чисто вещественной фазой в показателе.

В других книгах вы можете встретить формулы с другими знаками; вероятнее всего, в них используются углы, определенные по-иному.

Точнее, мы определим ^ R z (φ) как поворот физической системы на -φ вокруг оси z ; это то же самое, что повернуть систему координат на +φ.

Мы всегда вправе выбрать ось z вдоль направления поля при условии, конечно, что его направление не меняется и что больше полей нет.

Для большей строгости все эти рассуждения нужно было бы провести для малых поворотов ε. Раз каждый угол φ представляет собой сумму некоторого числа n таких поворотов, φ=nε, то ^R z(φ)=[R z(ε)] n, и общее изменение фазы в n раз превосходит изменение для малого угла 8 и поэтому пропорционально φ.