Ричард Фейнман - Том 3. Квантовая механика

Рассуждения, которыми мы только что пользовались, в равной степени применимы к поворотам на 180° вокруг любой оси в плоскости ху , хотя, конечно, повороты вокруг разных осей дадут для β разные числа. Но это единственное, чем они могут отличаться. В числе β имеется известный произвол, но, как только оно определено для какой-то одной оси в плоскости ху , оно определяется и для всех прочих осей. Принято выбирать β=0 для поворотов на 180° вокруг оси у .

Чтобы показать, что свобода такого выбора у нас есть, предположим, что мы решили, что β не равно нулю для поворота вокруг оси y ; тогда можно показать, что в плоскости ху существует какая - то другая ось, для которой соответствующая фаза будет нулем. Найдем фазовый множитель β Aдля оси А , образующей с осью у угол α, как показано на фиг. 4.7, а .

Фиг. 4.7. Поворот на 180° вокруг оси А (а) эквивалентен повороту на 180° вокруг оси у (б), за которым следует поворот вокруг оси z' (в).

(Для удобства на рисунке угол α отрицателен, но это неважно.) Если теперь мы возьмем прибор Т , первоначально направленный так же, как и S , а потом повернем его вокруг оси А на 180°, то его оси — назовем их х ", у ", z "— расположатся так, как на фиг. 4,7, а. Амплитуды по отношению к Т тогда станут

(4.23)

Но той же самой ориентации можно добиться двумя последовательными поворотами, показанными на фиг. 4.7, б и в . Возьмем сначала прибор U , повернутый по отношению к S на 180° вокруг оси у . Оси х ', у ' и z ' прибора U будут такими, как на фиг. 4.7, б , а амплитуды по отношению к U будут даваться формулой (4.22).

Заметьте теперь, что от U к T можно перейти, повернув прибор U вокруг «оси z», т. е. вокруг z', как показано на фиг. 4.7, в . Из рисунка видно, что требуемый угол вдвое больше угла α, но направлен в обратную сторону (по отношению к z'). Используя преобразование (4.19) с φ=-2α, получаем

(4.24)

Подставляя (4.22) в (4.24), получаем

(4.25)

Эти амплитуды, конечно, должны совпасть с полученными в (4.23). Значит, β A должно быть связано с α и β формулой

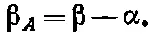(4.26)

Это означает, что если угол α между осью А и осью у (прибоpa S ) равен β то в преобразовании поворота на 180° вокруг оси А будет стоять β A=0.

Но коль скоро у какой - то из осей, перпендикулярных к оси z , может оказаться β=0, то ничто не мешает принять эту ось за ось у . Это всего лишь вопрос соглашения , и мы примем это в общем случае. Итог : для поворота на 180° вокруг оси у мы имеем

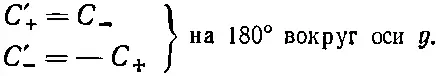(4.27)

Продолжая размышлять о поворотах вокруг оси у , перейдем теперь к матрице преобразования для поворотов на 90°. Мы в состоянии установить ее вид, оттого что знаем, что два последовательных поворота на 90° вокруг одной и той же оси — это то же самое, что один поворот на 180°. Напишем преобразование для 90° в самой общей форме:

(4.28)

Второй поворот на 90° вокруг той же оси обладал бы теми же коэффициентами:

(4.29)

Подставляя (4.28) в (4.29), получаем

(4.30)

Однако из (4.27) нам известно, что

так что должно быть

(4.31)

Этих четырех уравнений вполне хватает, чтобы определить все наши неизвестные а, b, с и d . Сделать это нетрудно. Посмотрите на второе и четвертое уравнения. Вы видите, что a 2= d 2, откуда либо a = d , либо a =- d . Но последнее отпадает, потому что тогда не выполнялось бы первое уравнение. Значит, d = a . А тогда сразу же выходит b =1/2 a и с=-1/2а. Теперь все выражено через а . Подставляя, скажем, во второе уравнение значения b и с, получаем

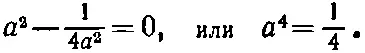
Из четырех решений этого уравнения только два приводят к детерминанту стандартной формы. Мы можем принять а=1/√2; тогда [15] Второе решение меняет все знаки у а, b, с, d и отвечает повороту на -270°.

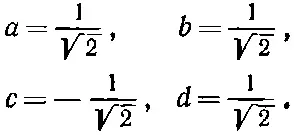
Иными словами, для двух приборов S и T при условии, что Т повернут относительно S на 90° вокруг оси у , преобразование имеет вид

(4.32)

Эти уравнения можно, конечно, разрешить относительно С +и С -; это даст нам преобразование при повороте вокруг оси у на -90°. Переставив еще и штрихи, мы напишем

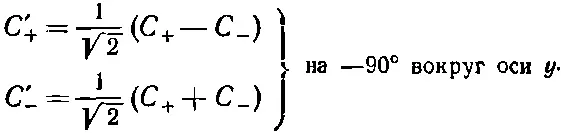(4.33)

Вы, пожалуй, подумаете: «Это становится смешным. Чему же нас теперь будут учить— поворотам на 47° вокруг оси у , потом на 33° вокруг x? Долго ли это будет продолжаться?» Нет, оказывается, я почти все рассказал. Зная только два преобразования — на 90° вокруг оси у и на произвольный угол вокруг оси z (как вы помните, именно с этого мы начали), — мы уже способны производить любые повороты.

Для иллюстрации предположим, что нас интересует поворот на угол α вокруг оси х . Мы знаем, как быть с поворотом на угол α вокруг оси z , но нам нужен поворот вокруг оси х . Как его определить? Сперва повернем ось z вниз до оси х , а это есть поворот на +90° вокруг оси у (фиг. 4.8).