Ричард Фейнман - Том 3. Квантовая механика

(4.15)

Для получения однозначных фаз мы просто умножаем каждый член в R на один и тот же фазовый множитель. В дальнейшем мы будем всегда предполагать, что наши матрицы были приведены к «стандартной форме»; тогда мы сможем пользоваться прямо формулой (4.11) без каких-либо добавочных фазовых множителей.

Теперь мы уже подготовлены к тому, чтобы отыскать матрицу преобразования R ji , связывающую два разных представления. Владея нашим правилом объединения поворотов и нашим предположением, что в пространстве нет предпочтительного направления, мы владеем ключом для отыскания матрицы любого произвольного поворота. Решение здесь только одно . Начнем с преобразования, которое отвечает повороту вокруг оси z . Пусть имеются два прибора S и Т , поставленных друг за другом вдоль одной прямой; оси их параллельны и смотрят из страницы на вас (фиг. 4.4, а ).

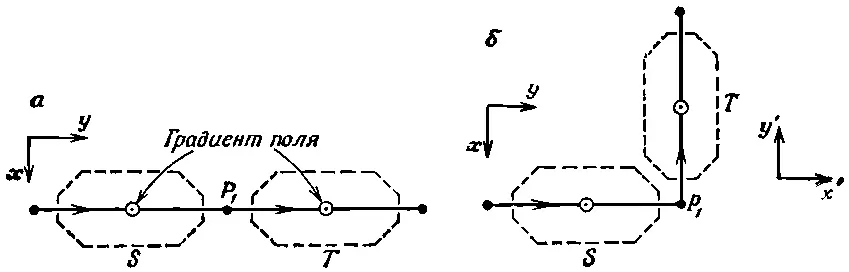
Фиг. 4.4. Поворот на 90° вокруг оси z.

Это их направление мы примем за ось z . Ясно, что если пучок в приборе S идет вверх (к + z ), то то же будет и в аппарате Т . Точно так же, если он в S идет вниз, то и в Т он направится вниз. Положим, однако, что прибор Т был повернут на какой-то угол, но его ось, как и прежде, параллельна оси прибора S , как на фиг. 4.4, б . Интуитивно хочется сказать, что пучок (+) в S будет по-прежнему переходить в пучок (+) в Т , потому что и поля, и их градиенты характеризуются тем же физическим направлением. И это вполне правильно. Точно так же и пучок (-) в S будет переходить в пучок (-) в Т . Тот же результат применим для любой ориентации Т в плоскости ху прибора S . Что же отсюда следует для связи между С ' +=<+T|ψ>, С ' -=<- T |ψ> и С +=<+ S |ψ>, С -=<- S |ψ>? Можно подумать, что любой поворот вокруг оси z «системы отсчета» базисных состояний оставляет амплитуды С ± пребывания «вверху» и «внизу» теми же, что и раньше, и написать С ' += С +и С' -= С -. Но это неверно . Все, что можно отсюда заключить, — это, что при таких поворотах вероятности оказаться в «верхнем» пучке приборов S и Т одинаковы, т. е.

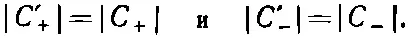
Но мы не вправе утверждать, что фазы амплитуд, относящихся к прибору Т , не могут в двух различных ориентациях а и б (фиг. 4.4) различаться.

Пары приборов, показанных на фиг. 4.4, на самом деле отличаются друг от друга, в чем можно убедиться следующим образом. Предположим, что мы перед прибором S поставили другой, создающий чистое (+ x )-состояние. (Ось х направлена на рисунке вниз.) Эти частицы расщеплялись бы в S на пучки (+ z ) и (- z ), но на выходе S (в точке Р 1) оба пучка снова соединялись бы и восстанавливали состояние (+ х ). Затем то же самое происходило бы в Т . Если бы за Т поставить третий прибор U , ось которого направлена по (+ х ), как показано на фиг. 4.5, а , то все частицы пошли бы в пучок (+) прибора U .

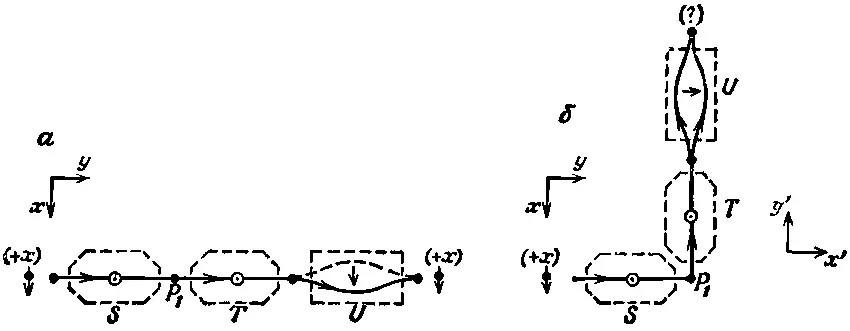
Фиг. 4.5. Частица в состоянии (+х) ведет себя в опытах а и б по-разному.

Теперь представим, что произойдет, если Т и U вместе повернуть на 90°, как показано на фиг. 4.5, б . Прибор Т опять будет пропускать все, что в него поступает, так что частицы, входящие в U , будут в (+ x )-состоянии по отношению к S . Но U теперь анализирует состояние (+ y ) (по отношению к S ), а это совсем не то, что раньше. (Из симметрии следует ожидать, что через него пройдет только половина частиц.)

Что же могло перемениться? Приборы Т и U по отношению друг к другу расположены одинаково. Могла ли измениться физика просто из-за того, что Т и U иначе ориентированы? Нет, гласит наше первоначальное предположение. Значит, различаться в двух случаях, показанных на фиг. 4.5, должны амплитуды по отношению к Т . То же должно быть, следовательно, и на фиг. 4.4. Частица должна как-то уметь узнавать, что в Р 1она завернула за угол. Как же она может об этом поведать? Что ж, остается только одно: величины С' +и С ' +в обоих случаях одинаковы, но могут — а на самом деле должны — обладать разными фазами . Мы приходим к заключению, что С ' +и С +должны быть связаны формулой

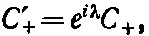
а С ' -и С -—формулой

где λ и μ — вещественные числа, которые как-то должны быть связаны с углом между S и Т .

В данный момент единственное, что мы можем сказать про λ и μ, — это то, что они не могут быть равны друг другу (кроме показанного на фиг. 4.5, а особого случая, когда Т и S ориентированы одинаково). Мы видели, что изменение всех амплитуд на одну и ту же фазу ни к каким физическим следствиям не приводит. По той же причине всегда можно добавить к λ и μ любое постоянное число — это тоже ничего не изменит. Значит, нам представляется возможность выбрать λ и μ равными плюс и минус одному и тому же числу. Всегда можно взять

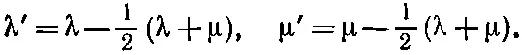
Тогда

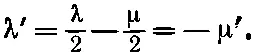
Итак, мы договоримся [12] Можно посмотреть на это и иначе. Мы просто производим преобразование к «стандартной форме», описанное в § 2, используя формулу (4.15). считать μ=-λ и придем к общему правилу, что поворот прибора, относительно которого ведется отсчет, вокруг оси z на какой-то угол приводит к преобразованию

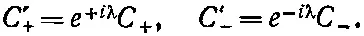(4.16)

Абсолютные значения одинаковы, а фазы различны. Эти-то фазовые множители и отвечают за различные результаты двух опытов, показанных на фиг. 4.5.

Теперь надо узнать закон, связывающий λ с углом между S и Т . Для одного случая ответ известен. Если угол — нуль, то и λ — нуль. Теперь предположим , что фазовый сдвиг λ есть непрерывная функция угла φ между S и Т (см. фиг. 4.4) при φ, стремящемся к нулю. По-видимому, это единственное разумное допущение. Иными словами, если свернуть Т с прямой линии S на малый угол ε, то и λ тоже будет малым числом, скажем m ε, где m — некоторый коэффициент. Мы пишем m ε, потому что можем доказать, что λ обязано быть пропорционально ε. Если бы мы поставили за T новый прибор Т, тоже образующий с Т угол ε, а с S тем самым образующий угол 2ε, то по отношению к Т мы бы имели