Ричард Фейнман - Том 3. Квантовая механика

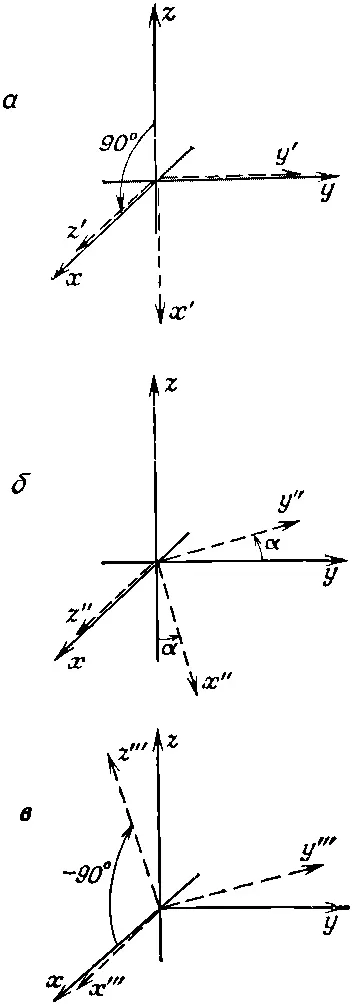
Фиг. 4.8. Поворот на угол α вокруг оси х равнозначен повороту на +90° вокруг оси у (а), за которым следует поворот ни а вокруг оси z' (б), вслед за которым происходит поворот на -90° вокруг оси у" (в).

Затем вокруг оси z ' повернемся на угол α. А потом повернемся на -90° вокруг оси у ". Итог этих трех поворотов тот же самый, что при повороте вокруг оси х на угол α. Таково свойство пространства.

(Все эти сочетания поворотов их результат очень трудно себе представить. Не правда ли, странно, что, живя в трех измерениях, мы все же с трудом воспринимаем, что произойдет, если сперва повернуться так, а потом еще как-нибудь. Вероятно, если бы мы были птицами или рыбами и если бы мы на собственном опыте знали, что бывает, когда все время крутишь разные сальто в пространстве, нам было бы легче воспринимать подобные вещи.)

Во всяком случае, давайте выведем преобразование для поворота на угол α вокруг оси х , пользуясь тем, что нам уже известно. При первом повороте на +90° вокруг оси у амплитуды следуют закону (4.32). Если повернутые оси обозначить х ', y' и z', то последующий поворот на угол α вокруг оси z переводит нас в систему отсчета х ", у ", z ", для которой

Последний поворот на -90° вокруг оси у " переводит нас в систему х '", у '", z '"; из (4.33) следует

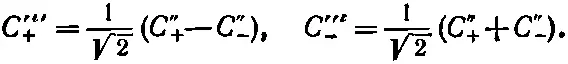
Сочетая эти два последних преобразования, получаем

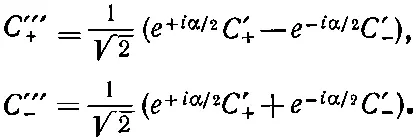
Подставляя сюда вместо С ' +и С' -(4.32), придем к полному преобразованию

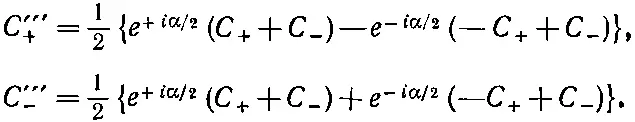
А если вспомнить, что

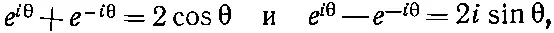
то эти формулы можно записать проще:

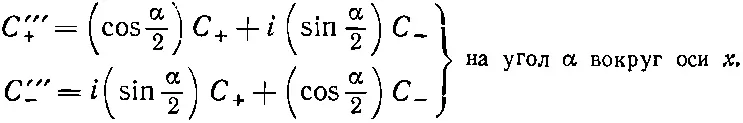(4.34)

Это и есть наше искомое преобразование для поворота вокруг оси х на любой угол α. Оно лишь чуть посложнее остальных.

Теперь уже понятно, как быть с произвольным поворотом. Во-первых, заметьте, что любая относительная ориентация двух систем координат может быть описана тремя углами (фиг. 4.9).

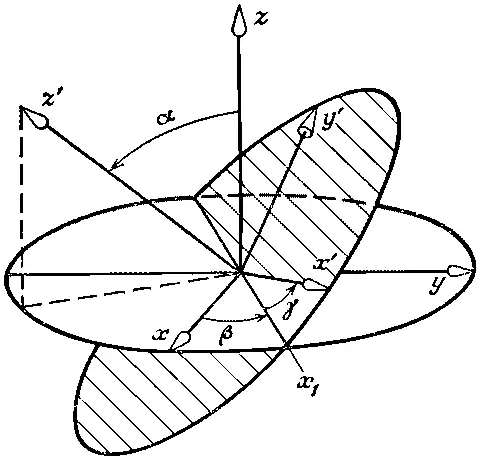
Фиг. 4.9. Ориентацию любой системы координат х', у', z' по отношению к другой системе х, у, z можно определить с помощью углов Эйлера α, β, γ.

Если есть система осей х ', у ', z ', ориентированных относительно х, у, z как угодно, то соотношение между ними можно описать тремя углами Эйлера α, β и γ, определяющими три последовательных поворота, которые переводят систему х, у , z в систему х ', у ', z '. Отправляясь от x, у , z, мы поворачиваем нашу систему на угол β вокруг оси z, перенося ось х на линию х '. Затем мы проводим поворот на угол α вокруг этой временной оси х 1, чтобы довести ось z до z '. Наконец, поворот вокруг новой оси z (т. е. вокруг z ') на угол γ переведет ось х 1в х ', а ось у в у ' [16] Нетрудно показать, что систему х, у, z можно перевести в систему х', у', z' следующими тремя поворотами вокруг первоначальных осей: 1) повернуть на угол γ вокруг первоначальной оси z; 2) повернуть на угол α вокруг первоначальной оси х; 3) повернуть на угол β вокруг первоначальной оси z. . Мы знаем преобразования для каждого из трех поворотов — они даются формулами (4.19) и (4.34). Комбинируя их в нужном порядке, получаем

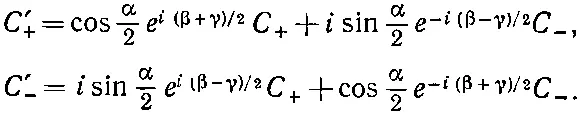(4.35)

Итак, начав просто с некоторых предположений о свойствах пространства, мы вывели преобразование амплитуды при любом повороте. Это означает, что если нам известны амплитуды того, что любое состояние частицы со спином 1/ 2перейдет в один из двух пучков прибора Штерна—Герлаха S с осями х, у, z , то мы можем подсчитать, какая часть перейдет в каждый пучок в приборе Т с осями х ', у ' и z '. Иначе говоря, если имеется состояние ψ частицы со спином 1/ 2, у которого амплитуды пребывания вверху и внизу по отношению к оси z системы координат х, у, z равны С +=<+|ψ> и С -=<-|ψ>, то тем самым мы знаем амплитуды С +и C -пребывания вверху и внизу по отношению к оси z ' любой другой системы х ', у ', z '. Четверка коэффициентов в (4.35) — это члены «матрицы преобразования», с помощью которой можно проецировать амплитуды частицы со спином 1/ 2в другие системы координат.

Теперь решим несколько примеров, чтобы посмотреть, как все это работает. Возьмем следующий простой вопрос. Пустим атом со спином 1/ 2через прибор Штерна—Герлаха, пропускающий только состояние (+ z ). Какова амплитуда того, что атом окажется в состоянии (+ x )? Ось + х — это все равно, что ось + z ' системы, повернутой на 90° вокруг оси у . Поэтому в этой задаче проще воспользоваться выражением (4.32), хотя, конечно, можно применить и полное уравнение (4.35). Поскольку С +=1 и С -=0, то получится С ' +=1/√2. Вероятности — это квадраты модулей этих амплитуд; таким образом, 50% шансов за то, что частица пройдет сквозь прибор, отбирающий состояние (+ х ). Если бы мы поинтересовались состоянием (- х ), то амплитуда оказалась бы -1/√2, что опять дало бы вероятность 1/ 2, чего и следовало ожидать из симметрии пространства. Итак, если частица находится в состоянии (+ z ), то ей в равной степени вероятно побывать в состояниях (+ x ) и (- х ). Но фазы противоположны.

Ось у тоже без претензий. Частица в состоянии (+ z ) имеет равные шансы быть в состоянии (+ у ) или (- у ). Но теперь (согласно формуле для поворота на -90° вокруг оси х ) амплитуды суть 1/√2 и - i /√2. В этом случае разница в фазах двух амплитуд уже не 180°, как было для (+ х ) и (- х ), а 90°. В этом-то и проявляется различие между х и у .

Вот еще пример. Пусть нам известно, что частица со спином 1/ 2находится в состоянии ψ, поляризованном вверх относительно оси А , определяемой углами θ и φ (фиг. 4.10).