Ричард Фейнман - Том 3. Квантовая механика

Для следующего шага нужно еще немного информации. Пусть мы добавили третий прибор (назовем его U ), стоящий вслед за Т под каким-то произвольным углом (фиг. 4.3, а ).

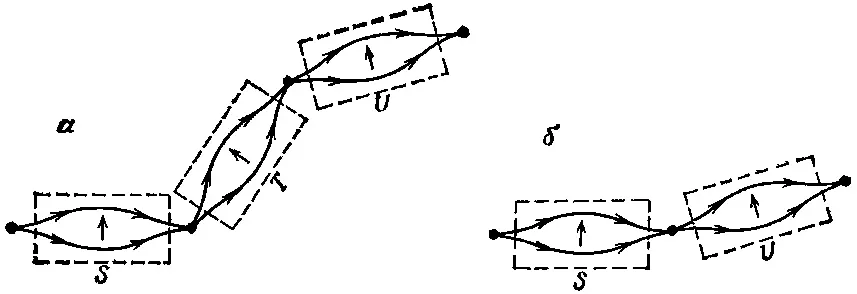
Фиг. 4.3. Если Т «открыт до отказа», то б эквивалентно а.

(Все это начинает выглядеть устрашающе, но в этом-то и прелесть отвлеченного мышления: самые сверхъестественные опыты можно ставить, просто проводя новые линии!) Что же представляет собой преобразование S → Т → U ? Фактически нас интересует амплитуда перехода из некоторого состояния по отношению к S к некоторому другому состоянию по отношению к U , если известны преобразования от S к Т и от Т к U . Поинтересуемся сперва опытом, в котором в Т открыты оба канала. Ответ можно получить, дважды подряд применяя (4.5). Для перехода от S -представления к T -представлению имеем

(4.6)

где верхние индексы TS нужны, чтобы отличать это R от R UT , когда мы будем переходить от Т к U .

Обозначая амплитуды появления атома в базисных состояниях представления U через C " k , можно связать их с T -амплитудами, применяя (4.5) еще раз; получим

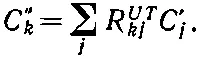(4.7)

Теперь можно из (4.6) и (4.7) получить преобразование от S прямо к U . Подставляя С ' j из (4.6) в (4.7), имеем

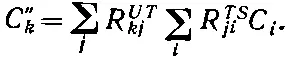(4.8)

Или, поскольку в R UT kj отсутствует i , можно поставить суммирование по i впереди и написать

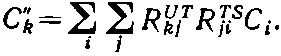(4.9)

Это и есть формула двойного преобразования.

Заметьте, однако, что, пока пучки в Т не загораживаются, состояния на выходе из Т те же , что и при входе в него. Мы могли бы с равным успехом делать преобразования из S -представления прямо в представление U . Это значило бы, что прибор U поставлен прямо за S , как на фиг. 4.3, б . В этом случае мы бы написали

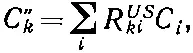
где R US ki — коэффициенты, принадлежащие этому преобразованию. Но ясно, что (4.9) и (4.10) должны приводить к одинаковым амплитудам С " k , причем независимо от того, каково было то начальное состояние φ, которое снабдило нас амплитудами С i . Значит, должно быть

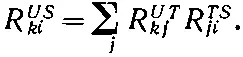(4.11)

Иными словами, для любого поворота S → U базиса, если рассматривать его как два последовательных поворота S → Т и Т → U , можно получить матрицу поворота R US ki из матриц двух частных поворотов при помощи формулы (4.11). Если угодно, (4.11) следует прямо из (4.1) и представляет собой лишь другую запись формулы:

Для полноты добавим еще следующее. Но не думайте, что это будет что-то страшно важное; если хотите, переходите, не читая, прямо к следующему параграфу. Надо сознаться, что то, что мы сказали, не совсем верно. Мы не можем на самом деле утверждать, что (4.9) и (4.10) обязаны привести к абсолютно одинаковым амплитудам. Одинаковыми должны оказаться только физические результаты ; сами же амплитуды могут отличаться на общий фазовый множитель типа e iδ, не меняя результатов никаких расчетов, касающихся реального мира. Иначе говоря, вместо (4.11) единственное, что можно утверждать, — это

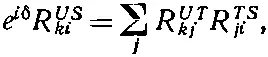(4.12)

где δ — какая - то вещественная постоянная величина. Смысл этого добавочного множителя е iδ, конечно, в том, что амплитуды, которые мы получим, пользуясь матрицей R US , могут все отличаться на одну и ту же фазу ( е - i δ) от амплитуд, которые получились бы из двух поворотов R UT и R TS . Но мы знаем, что если все амплитуды изменить на одинаковую фазу, то это ни на чем не скажется. Так что при желании можно этот фазовый множитель просто игнорировать. Оказывается, однако, что если определить нашу матрицу поворота особым образом, то этот фазовый множитель вообще не появится: δ в (4.12) всегда будет нулем. Хотя это и не отражается на наших дальнейших рассуждениях, мы беремся это быстро доказать, пользуясь математической теоремой о детерминантах. [А если вы до сих пор мало знакомы с детерминантами, то не следите за доказательством и прямо переходите к определению (4.15).]

Во-первых, следует напомнить, что (4.11) — это математическое определение «произведения» двух матриц. (Просто очень удобно говорить « R US есть произведение R UT и R TS ».) Во-вторых, существует математическая теорема (которую для используемых здесь матриц 2×2 вы легко докажете), утверждающая, что детерминант «произведения» двух матриц есть произведение их детерминантов. Применив эту теорему к (4.12), получим

(4.13)

(Мы отбрасываем нижние индексы, они здесь ничего полезного нам не сообщают.) Да, слева стоит 2δ! Вспомните, что мы имеем дело с матрицами 2x2; каждый член в матрице R US ki умножен на е i δ, а каждый член в детерминанте (состоящий из двух множителей) получается умножением на е i 2δ. Извлечем из (4.13) корень и разделим на него (4.12):

(4.14)

Добавочный фазовый множитель исчез.

Дальше оказывается, что если мы хотим, чтобы все наши амплитуды в любом заданном представлении были нормированы (а это, как вы помните, означает, что ∑ i<���φ|i>=1, то у всех матриц поворота детерминанты окажутся чисто мнимыми экспонентами, наподобие е i α. (Мы не будем этого доказывать; вы сами потом увидите, что это всегда так.) Значит, мы сможем, если захотим, выбрать все наши матрицы поворота R так, чтобы фаза их получалась однозначно, взяв Det R =1. Это будет делаться так. Пусть мы каким-то произвольным образом определили матрицу поворота R . Возьмем за правило «приводить» ее к «стандартной форме», определяя