Ричард Фейнман - КЭД – странная теория света и вещества

В случае поглощающих свет веществ малые стрелки направлены под тупым углом к основной стрелке (см. рис. 69, б ). В итоге результирующая стрелка оказывается короче основной, что указывает на меньшую вероятность прохождения фотона сквозь частично прозрачное стекло, чем сквозь прозрачное.

Таким образом получается, что все явления, а также произвольные числа, о которых говорилось на первых двух лекциях, например, частичное отражение с амплитудой 0,2, «замедление» света в воде или в стекле, и т. д., более детально объясняются всего лишь тремя основными действиями – всего тремя, но объясняющими на самом деле и почти все остальное.

Трудно поверить, что почти все видимое бесконечное разнообразие Природы проистекает из монотонного повторения трех основных действий. Но это так. Я немного расскажу о том, как возникает это разнообразие.

Мы можем начать с фотонов (см. рис. 70). Какова вероятность того, что два фотона, выйдя из точек 1 и 2 пространства-времени, попадут в два детектора в точках 3 и 4 ? Для осуществления этого события имеются два основных способа, и каждый состоит из двух независимых процессов: фотоны могут лететь прямо: Р ( 1–3 )× Р ( 2–4 ) – или «крест-накрест»:

Р ( 1–4 )× Р ( 2–3 ). Получающиеся таким образом амплитуды обеих возможностей складываются, и возникает (как мы видели на второй лекции) интерференция: длина результирующей стрелки меняется в зависимости от относительного положения пространственно-временных точек.

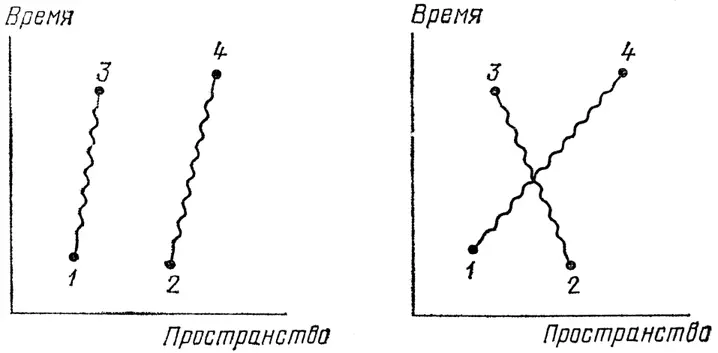
Рис. 70 . Амплитуда попадания фотонов из точек 1 и 2 пространства-времени в точки 3 и 4 может быть приближенно найдена, если рассмотреть два изображенных на рисунке основных способа осуществления этого события: Р ( 1–3 )× Р ( 2–4 ) и Р ( 1–4 )× Р ( 2–3 ). При изменении относительного положения точек 1, 2, 3 и 4 в различной степени проявляется интерференция.

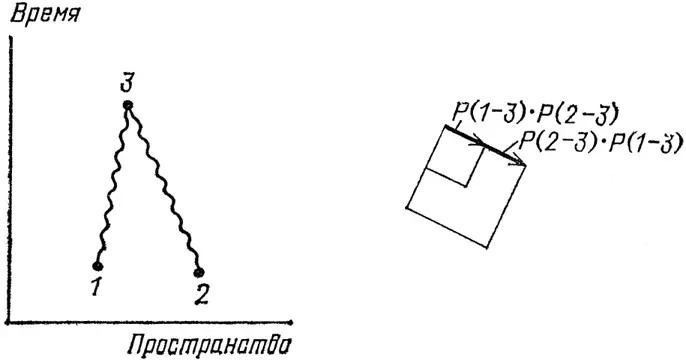
Рис. 71. Если совместить точки 4 и 3, две стрелки Р(1–3)×Р(2–3) и Р(2–3)×Р(1–3) окажутся одинаковыми как по дли-не, так и по направлению. При сложении они выстраиваются в одну линию и образуют стрелку удвоенной длины (квадрат которой при этом возрастает в четыре раза). Таким образом, фотоны стремятся попасть в одну пространственно-временную точку. При увеличении числа фотонов этот эффект усиливается. Он лежит в основе действия лазера.

Что произойдет, если мы совместим точки 3 и 4 в пространстве-времени (см. рис. 71)? Скажем, оба фотона попадают в точку 3 . Посмотрим, как это скажется на вероятности события. В данном случае мы имеем Р ( 1–3 )× Р ( 2–3 ) и Р ( 2–3 )× P ( 1–3 ) – две одинаковые стрелки. При сложении их длина удвоится, что приведет к учетверению квадрата длины результирующей стрелки по сравнению с квадратом длины одной стрелки. Так как две стрелки одинаковы, они всегда «выстраиваются в одну линию». Другими словами, интерференция не флуктуирует при изменении положений точек 1 и 2 , она всегда положительна. Если бы мы не учитывали такой всегда положительной интерференции двух фотонов, то мы ожидали бы, что вероятность возрастает в среднем в два раза. Вместо этого вероятность всегда возрастает в четыре раза. Когда мы имеем дело с большим числом фотонов, эта превосходящая наши ожидания вероятность возрастает еще сильнее.

Это приводит к целому ряду практических следствий. Можно сказать, что фотоны стремятся попасть в одинаковые условия или «состояния». («Состояние» – это определенная пространственная зависимость амплитуды нахождения фотона.) Вероятность того, что атом излучит фотон, возрастает, если уже имеются фотоны в таком состоянии, в котором они могут быть излучены данным атомом. Это явление, получившее название «вынужденного излучения», открыл Эйнштейн, когда, предложив фотонную модель света, он положил начало квантовой теории. Работа лазеров основана на этом явлении.

Такое же рассуждение применимо и к нашим фальшивым электронам со спином нуль. Но в реальном мире, где электроны поляризованы, происходит нечто совсем другое: две стрелки, Е ( 1–3 )× Е ( 2–4 ) и Е ( 1–4 )× Е ( 2–3 ), вычитаются одна из другой – т. е. перед сложением одна из них поворачивается на 180°. Если точки 3 и 4 совпадают, стрелки одинаковы как по длине, так и по направлению, и при вычитании взаимно уничтожаются (см. рис. 72). Это означает, что, в отличие от фотонов, электроны не любят попадать в одно место, они бегут друг от друга как от чумы. Два электрона с одинаковой поляризацией не могут оказаться в одной точке пространства-времени – это явление называется «принципом запрета».

Этот принцип запрета, оказывается, лежит в основе великого разнообразия химических свойств атомов. Один протон обменивается фотонами с танцующим вокруг него одним электроном – это атом водорода. Два протона одного ядра обмениваются фотонами с двумя электронами (поляризованными в противоположных направлениях) – это атом гелия. Видите ли, у химиков сложный способ счета: вместо того чтобы говорить «один, два, три, четыре, пять протонов», они говорят: «водород, гелий, литий, бериллий, бор».

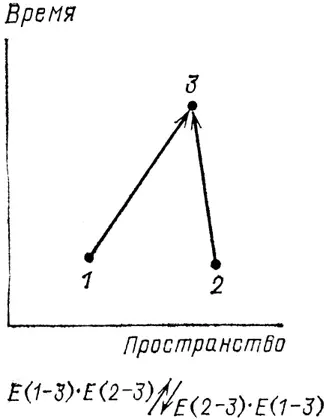
Рис. 72. Если два электрона (с одинаковой поляризацией) пытаются занять одну и ту же точку в пространстве-времени, интерференция всегда отрицательна. (Так проявляет-ся поляризация электронов.) Это значит, что две одинаковые стрелки Е(1–3)×Е(2–3) и Е(2–3)×Е(1–3) должны вычитаться друг из друга, в результате дли-на результирующей стрелки зануляется. Такое нежелание двух электронов занимать одно место в пространстве-времени называется «принципом запрета». Этим объясняется большое разнообразие атомов во Вселенной.

У электрона есть только два состояния поляризации, поэтому в атоме, где три протона ядра обмениваются фотонами с тремя электронами – он называется атомом лития – третий электрон расположен дальше от ядра, чем два других (занявших ближайшее возможное место), и реже обменивается фотонами. Такой электрон легко отрывается от своего ядра под действием фотонов других атомов. Большое число таких атомов, расположенных поблизости друг от друга, легко теряют свой собственный третий электрон, и получается целое море электронов, плавающих вокруг атомов. Если к этому морю электронов приложить слабую электрическую силу (фотоны), в нем образуется поток электронов – я описываю, как металлический литий проводит электрический ток. Водород и гелий не отдают свои электроны другим атомам. Они «изоляторы».