Ричард Фейнман - КЭД – странная теория света и вещества

– Этап 2: Фотон летит от источника к одной из точек в стекле.

– Этап 3: Фотон рассеивается электроном в этой точке.

– Этап 4: Новый фотон летит к детектору.

Мы будем считать, что амплитуды для этапов 2 и 4 (фотон летит к точке в стекле и от нее) имеют длину, равную 1, и нулевой угол поворота, поскольку можно предположить, что свет не теряется и не рассеивается между стеклом и детектором. Амплитуда этапа 3 (рассеяния фотона электроном) является константой – S (сжатие и поворот на некоторую величину) – и одинакова всюду внутри стекла. (Эта величина, как я отмечал ранее, различна для разных веществ. Для стекла поворот S равен 90°.) Следовательно, из четырех стрелок, которые нужно перемножить, только стрелка для этапа 1 – амплитуда излучения в определенный момент – будет разной для разных путей.

Момент, когда фотон должен вылететь из источника, чтобы достичь детектора А в момент Т (см. рис. 68, б ), будет разным для шести различных путей. Фотон, рассеянный в точке Х 2, должен быть излучен несколько раньше , чем фотон, рассеянный в Х 1, поскольку его путь длиннее. Поэтому стрелка в Т 2 повернута на несколько больший угол, чем в T 1 – ведь пока время идет, амплитуда излучения фотона в определенный момент для монохроматического источника вращается против часовой стрелки. Это же относится к каждой стрелке вплоть до Т 6: все шесть стрелок имеют одинаковую длину, но повернуты на разные углы, т. е. указывают в разных направлениях, поскольку относятся к фотону, излучаемому источником в разные моменты времени.

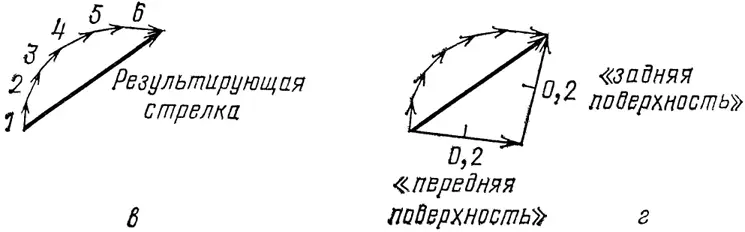
Рис. 68, в – г. Закончив умножать стрелки для каждой возможности, получим стрелки, показанные на рис. в. Они короче, чем стрелки на рис. б, каждая повернута на 90° (в соответствии с рассеивающими свойствами электронов стекла). При сложении эти шесть стрелок образуют дугу, результирующая стрелка является хордой этой дуги. Можно получить такую же результирующую стрелку, нарисовав две радиальные стрелки (на-правленные по радиусам дуги (см. рис. г) и «вычтя» одну из другой, т. е. повернув стрелку «передней поверхности» в обратную сторону и сложив со стрелкой «задней поверхности». Эта замена была использована для упрощения изложения в первой лекции.

Сжимая стрелку, относящуюся к T 1, в число раз, предписанное этапами 2, 3 и 4 , и поворачивая ее на 90°, предписанные этапом 3 , получаем стрелку 1 (см. рис. 68, в ). Следовательно, стрелки 1 …., 6 имеют одинаковую (уменьшенную) длину и повернуты друг относительно друга на такой же угол, что и стрелки, характеризующие излучение фотона в Т 1…., Т 6.

Сложим теперь стрелки 1…., 6 . Последовательно соединяя стрелки, получим нечто вроде дуги окружности. Результирующая стрелка служит хордой этой дуги. Длина результирующей стрелки возрастает по мере утолщения стекла: больше толщина стекла – больше слоев, больше стрелок – и получается большая дуга окружности. И так до тех пор, пока не получится половина окружности (результирующая стрелка в этом случае является диаметром). Затем, при нарастающей по-прежнему толщине стекла, длина результирующей стрелки начинает убывать , дуга превращается в полную окружность, и начинается новый период. Квадрат длины результирующей стрелки равен вероятности, которая за цикл колеблется в пределах от нуля до 16 %.

Для получения этого ответа можно применить математический трюк (см. рис. 68, г ): соединив стрелками центр окружности с хвостом стрелки 1 и головой стрелки 6, получим две радиальные стрелки. Если повернуть первую из них на 180° и сложить со второй (т. е. «вычесть» первую из второй), получим прежнюю результирующую стрелку! Именно это я и делал на первой лекции: эти два радиуса и есть те две стрелки, которые, как я говорил, соответствуют отражению от «передней поверхности» и «задней поверхности». Каждая радиальная стрелка имеет хорошо известную нам длину 0,2 [24].

Таким образом, мы можем правильно вычислить вероятность частичного отражения, предположив (ложно), что все отражение происходит только от передней и задней поверхности. При таком интуитивно простом расчете стрелки «передней поверхности» и «задней поверхности» – это дающие правильный ответ математические построения. В то же время проделанный нами только что анализ – в пространстве-времени со стрелками, образующими часть окружности, – более точно показывает, что происходит в действительности: частичное отражение – это рассеяние света электронами внутри стекла.

Теперь разберемся со светом, проходящим сквозь стекло. Во-первых, имеется некоторая амплитуда того, что фотон пролетит сквозь стекло, ни разу не столкнувшись с электронами (см. рис. 69, а ). В смысле длины это самая важная стрелка. Но имеются еще шесть других возможных путей, которыми фотон может попасть в детектор под стеклом: фотон может столкнуться в точке X 1, а новый фотон рассеется в В ; фотон может столкнуться в точке Х 2, а новый фотон рассеется в В , и т. д. Все шесть стрелок такой же длины, как и стрелки, образующие дугу в предыдущем примере: она определяется той же самой амплитудой рассеяния фотона в среде S . На этот раз все шесть стрелок направлены одинаково, так как все шесть путей с одним актом рассеяния имеют одинаковую длину. В таких прозрачных веществах, как стекло, эти малые стрелки направлены под прямым углом к основной стрелке. В результате сложения малых стрелок и основной стрелки получаем результирующую стрелку такой же длины, что и основная, но повернутую на небольшой угол. Чем толще стекло, тем больше будет малых стрелок и тем сильнее будет повернута результирующая стрелка. Так устроена фокусирующая линза; расположив на более коротких путях добавочные слои стекла, можно добиться того, чтобы результирующие стрелки для всех путей были направлены одинаково.

Эффект был бы таким же, если бы фотоны в стекле распространялись медленнее, чем в воздухе: результирующая стрелка сделала бы дополнительный поворот. Вот почему раньше я говорил, что свет в стекле (или воде) распространяется медленнее, чем в воздухе. В действительности «замедление» света объясняется добавочным вращением, связанным с рассеянием света атомами стекла (или воды). Величина этого добавочного поворота в данном веществе называется «показателем преломления вещества» [25].

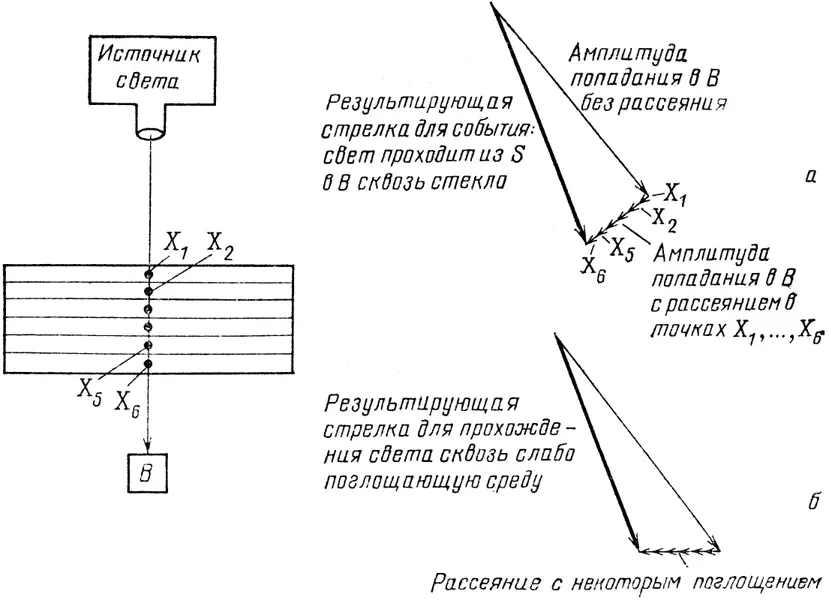
Рис. 69 . Наибольший вклад в амплитуду прохождения света через стеклянную пластинку в детектор в точке В вносит часть, соответствующая отсутствию рассеяния на электронах стекла ( а ). К этой стрелке мы прибавляем шесть маленьких стрелок, отвечающих рассеянию света в каждом из слоев в точках X 1 …., Х 6 . Эти шесть стрелок имеют одинаковую длину (поскольку всюду внутри стекла амплитуда рассеяния одинакова), их направления совпадают (поскольку все пути от источника через любую из точек X к детектору имеют одинаковую длину). Сложив большую стрелку с маленькими, видим, что результирующая стрелка повернута сильнее, чем если бы свет распространялся прямо. По этой причине нам представляется, что путь через стекло занимает больше времени, чем через вакуум или воздух. Величина поворота результирующей стрелки, вызванного электронами вещества, называется «показателем преломления». В случае прозрачных веществ маленькие стрелки направлены под прямым углом к основной стрелке. (На самом деле при учете двойного и тройного рассеяния они несколько отклоняются, так что длина результирующей стрелки не превышает длины основной стрелки: Природа устроена так, что мы не можем получить на выходе из пластинки больше света, чем на входе.) В случае неполностью прозрачных (частично поглощающих свет) веществ маленькие стрелки направлены под тупым углом к основной стрелке. Поэтому результирующая стрелка получается значительно короче, чем ожидалось ( б ). Такая укороченная результирующая стрелка означает уменьшение вероятности прохождения фотона сквозь частично прозрачное вещество.