Ричард Фейнман - КЭД – странная теория света и вещества

В качестве первого примера давайте вычислим вероятность того, что два электрона попадут из пространственно-временных точек 1 и 2 в точки 3 и 4 (см. рис. 59). Такое событие может произойти несколькими способами. Первый способ состоит в том, что электрон из точки 1 летит в точку 3 (надо подставить 1 и 3 в формулу Е ( А – В ), я запишу это в виде Е ( 1–3 ), а электрон из точки 2 летит в точку 4 . Поскольку это два независимых подпроцесса, надо умножить одну стрелку на другую, чтобы получить стрелку для этого первого способа, которым могло произойти событие. Поэтому мы пишем такую формулу для стрелки «первого способа»: Е ( 1–3 )× Е ( 2–4 ).

Другой способ, которым может произойти данное событие: электрон из точки 1 летит в точку 4 , а электрон из точки 2 – в точку 3. Это опять два независимых подпроцесса. Стрелка «второго способа» равна Е ( 1–4 )× Е ( 2–3 ), и мы складываем ее со стрелкой «первого способа» [19]. Это хорошее приближение для амплитуды данного события.

Чтобы провести более точный расчет, который бы лучше согласовывался с результатами эксперимента, мы должны рассмотреть другие способы, которыми может произойти данное событие. Например, в каждом из двух основных способов один электрон мог отправиться в какое-то новое и чудесное место и испустить фотон (см. рис. 60). Тем временем другой электрон мог попасть в какое-то другое место и поглотить там этот фотон. Вычисление амплитуды первого из этих новых способов заключается в умножении следующих амплитуд: электрон летит из точки 1 в новое и чудесное место 5 (где он излучает фотон), затем летит из 5 в 3 ; другой электрон летит из точки 2 в другое место 6 (где он поглощает фотон), затем летит из 6 в 4 . Мы не должны также забывать про амплитуду попадания фотона из 5 и 6 . Я напишу амплитуду такого способа осуществления события в первоклассном математическом виде, а вы можете следить: E ( 1–5 )× j × E ( 5–3 )× E ( 2–6 )× j × E ( 6–4 )× P ( 5–6 ) – множество сжатий и поворотов. (Предоставляю вам самим написать формулу для другого случая, когда электрон из точки 1 попадает в точку 4 , а электрон из точки 2 попадет в точку 3 .) [20]

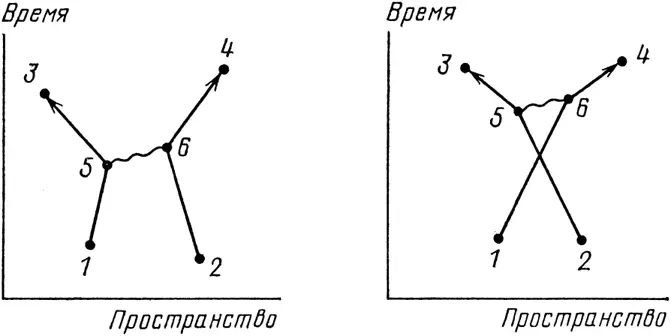
Рис. 60. Вот два других способа, которыми может произойти событие на рис. 59: на каждом рисунке в точке 5 испускается, а в точке 6 поглощается фотон. Конечные условия здесь такие же, как и в двух предыдущих случаях – два электрона входят и два выходят – так что результаты неотличимы. Поэтому стрелки для этих «других способов» надо прибавить к стрелкам для всех способов на рис. 59, тогда получится еще лучшее приближение для результирующей стрелки всего события.

Но постойте: положение точек 5 и 6 может быть любым в пространстве и времени, не правда ли, – и надо вычислить и сложить стрелки для всех этих положений. Как видите, предстоит немало работы. Дело не в том, что правила очень сложны – это похоже на игру в шашки: правила простые, но вы применяете их снова и снова. Итак, наши сложности при расчете связаны с тем, что нужно нагромоздить целую кучу стрелок. Вот почему студенты целых четыре года учатся делать это эффективно – а ведь мы рассматриваем легкую задачу! (Когда задачи становятся слишком трудными, мы решаем их с помощью компьютера!)

Я хотел бы отметить следующее относительно поглощения и излучения фотонов. Если точка 6 расположена позже, чем точка 5 , мы можем сказать, что фотон излучился в 5 и поглотился в 6 (см. рис. 61). Если точка 6 расположена раньше, чем 5 , мы, вероятно, предпочли бы сказать, что фотон излучился в 6 и поглотился в 5 . Но с таким же успехом мы могли бы сказать, что фотон движется вспять во времени! Нам, однако, не надо беспокоиться о том, в каком направлении в пространстве-времени летит фотон; все это учтено в формуле для Р ( 5–6 ), и мы говорим, что произошел «обмен» фотоном. Разве не замечательно, что Природа так проста! [21]

Далее, вдобавок к обмену фотоном между точками 5 и 6 возможен обмен другим фотоном – между точками 7 и 8 (см. рис. 62). Я слишком устал, чтобы выписывать все основные действия, стрелки которых должны быть перемножены, но, как вы могли заметить, каждая прямая линия дает Е ( А – В ), каждая волнистая линия дает Р ( А – В ), а каждое взаимодействие дает j . Итак, имеются шесть Е ( А – В ), два Р ( А – В ) и четыре j – и так для любых возможных точек 5, 6, 7 и 8 ! Это дает миллиарды маленьких стрелочек, которые надо перемножить и потом сложить!

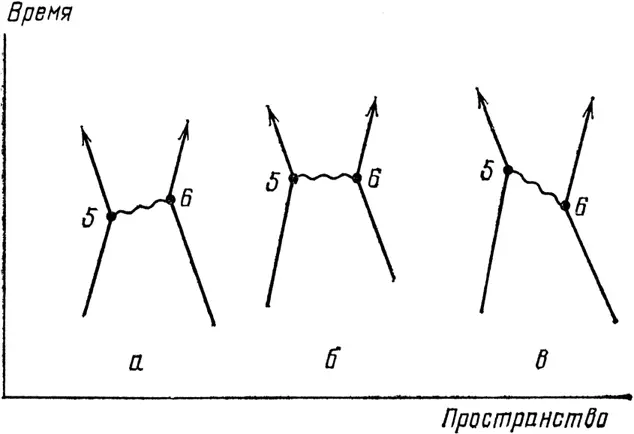
Рис. 61. Поскольку у света имеется амплитуда лететь быстрее или медленнее обычной скорости света, можно считать, что во всех трех примерах фотоны излучались в точке 5 и поглощались в точке 6. И это несмотря на то, что в примере б фотон был излучен и поглощен в одно и то же время, а в примере в был излучен позже, чем поглощен. В последней ситуации вы, может быть, предпочли бы сказать, что фотон был излучен в 6 и поглощен в 5, ведь иначе фотон должен был бы лететь вспять во времени! Постольку поскольку это касается вычислений (и Природы), это все равно (и все возможно). Поэтому мы говорим просто, что произошел «обмен» фотоном, и подставляем пространственно-временные положения в формулу для Р(А – В).

Кажется, вычисление амплитуды этого простого события – дело безнадежное. Однако если вы студент и вам надо получить диплом, то вы работаете.

Но надежда на успех есть. Она основана на этом магическом числе j . В первых двух способах, которыми может произойти событие, j не фигурирует; в следующем способе имеется j × j , а в последнем рассмотренном нами – j × j × j × j . Так как j × j меньше 0,01, это означает, что длина стрелки для этого способа, вообще говоря, составляет меньше 1 % длины стрелки для первых двух способов. Стрелка с j × j × j × j будет меньше, чем 1 % от 1 %, т. е. одна десятитысячная часть в сравнении со стрелками, не содержащими j . Если у вас достаточно компьютерного времени, можете рассмотреть возможности, содержащие j 6 – одну миллионную часть, при этом ваши расчеты будут соответствовать точности экспериментов. Вот так и рассчитываются простые события. Именно таким образом все и устроено!

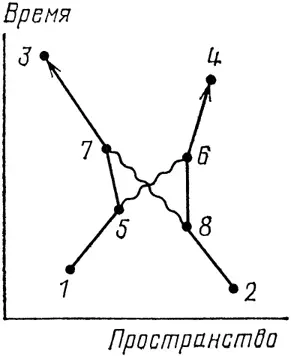
Рис. 62. Событие на рис. 59 может произойти еще одним способом (третьим): путем обмена двумя фотонами. Для этого способа (как мы увидим подробнее ниже) имеется множество диаграмм, одна из которых здесь показана. Стрел-ка для этого способа учитывает все возможные положения промежуточных точек 5, 6, 7 и 8, и по-этому вычислять ее очень трудно. Поскольку j меньше, чем 0,1, дли-на этой стрелки, вообще говоря, меньше, чем одна десятитысячная (так как в процессе происходят четыре взаимодействия) – по срав-нению с не содержащими j стрелками «первого способа» и «второго способа» на рис. 59.