Ричард Фейнман - 7. Физика сплошных сред

§ 4. Отраженная и преломленная волны

Теперь мы готовы применить наши граничные условия к вол­нам, перечисленным в § 2, где мы получили:

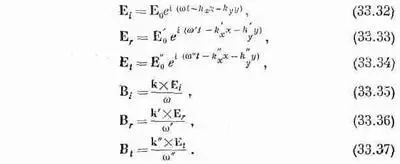
Нами получены еще кое-какие сведения: вектор Еперпендику­лярен для каждой волны вектору распространения k.

Полученный результат будет зависеть от направления век­тора Е(«поляризации») в падающей волне. Анализ сильно упро­стится, если мы рассмотрим отдельно случай, когда вектор Е параллелен «плоскости падения» (т. е. плоскости ху), и случай, когда он перпендикулярен к ней. Волна с любой другой поляри­зацией будет просто линейной комбинацией этих волн. Другими словами, отраженные и преломленные интенсивности для различных поляризаций будут разными и легче всего отобрать два простейших случая и отдельно рассмотреть их.

Я подробно проанализирую случай падающей волны, пер­пендикулярной к плоскости падения, а потом просто опишу вам, что получается в других случаях. Я немного жульничаю, рас­сматривая простейший пример, однако в обоих случаях прин­цип один и тот же. Итак, мы считаем, что вектор Е i имеет только z-компоненту, а поскольку все векторы Есмотрят в одном и том же направлении, векторный значок можно опустить.

Оба материала изотропны, поэтому вынужденные колеба­ния зарядов в материале будут происходить в направлении оси z и у полей Ев преломленной и отраженной волнах тоже будет только одна z-компонента. Таким образом, для всех волн Е х и Е y , Р х и Р y равны нулю. Направления векторов Еи Вв этих волнах показаны на фиг. 33.6.

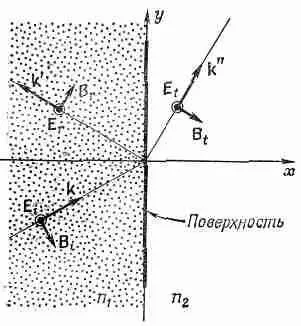
Фиг. 33.6. Поляризации отражен­ной и преломленной волн, когда поле Е в падающей волне перпендикулярно к плоскости падения.

(Здесь мы изменили нашему пер­воначальному намерению все получить из уравнений. Этот результат также можно было бы получить из граничных усло­вий, однако, используя физические аргументы, мы избежали больших алгебраических выкладок. Когда у вас будет свобод­ное время, посмотрите, можно ли его действительно вывести из уравнений. Он, разумеется, согласуется с уравнениями; просто мы не доказали, что отсутствуют другие возможности.)

Теперь наши граничные условия [уравнения (33.26) — (33.31)] должны дать соотношения между компонентами Еи Вв областях 1 и 2. В области 2 у нас есть только одна преломлен­ная волна, а вот в области 1 — их две. Какую же из них нам взять? Поля в области 1 будут, разумеется, суперпозицией полей падающей и отраженной волн. (Поскольку каждое удовлетворяет уравнениям Максвелла, то им удовлетворяет и сумма.) Поэтому, когда мы используем граничные условия, нужно помнить, что

E 1=E i+E r, E 2=E t

я аналогично для В.

Для поляризаций, которыми мы сейчас занимаемся, уравне­ния (33.26) и (33.28) не дают никакой новой информации, и только уравнение (33.27) поможет нам. Оно говорит, что на границе, т. е. при х=0:

E i +E r =E t .

Таким образом, мы получаем уравнение

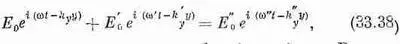
которое должно выполняться для любого t и любого у. Возьмем сначала y=0. Для этого значения уравнение (33.38) превра­щается в

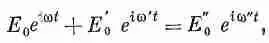
согласно которому два осциллирующих члена равны третьему. Это может произойти, только когда частоты всех осцилляции одинаковы. (Невозможно, сложив три или какое-то другое число подобных членов с различными частотами, получить для любого момента времени в результате нуль.) Итак,

w"=w'=w, (33.39)

как это и было нам всегда известно, т. е. частоты преломленной и отраженной волн те же самые, что и падающей.

Если бы мы предположили это с самого начала, то несом­ненно избежали бы многих трудностей, но мне хотелось пока­зать вам, что тот же самый результат можно получить и из урав­нений. А вот когда перед вами будет стоять реальная задача, лучше всего пускать в оборот сразу все, что вы знаете. Это избавит вас от лишних хлопот.

По определению абсолютная величина k задается равенством k 2=n 2w 2/с 2, поэтому

А теперь обратимся к уравнению (33.38) для t =0. Используя снова те же рассуждения, что и прежде, но на сей раз основы­ваясь на том, что уравнения должны быть справедливы при всех значениях у, мы получаем

k" y=k' y=k y. (33.41)

Из формулы (33.40) k' 2=k 2, так что

k' 2 x+k' 2 y=k 2 x+k 2 y. Комбинируя это с (33.41), находим

k' 2 x=k 2 x, или k' x =+k x . Знак плюс не имеет никакого смысла; он не дает нам никакой отраженной волны, а лишь другую падающую волну, и с самого начала мы говорили, что будем решать задачу с единственной падающей волной, так что

k' x =-k x . (33.42)

Два соотношения (33.41) и (33.42) говорят нам, что угол отра­жения равен углу падения, как это и ожидалось (см. фиг. 33.3). Итак, в отраженной волне

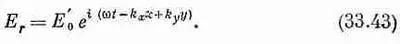
Для преломленной волны мы уже получали

Их можно решить и в результате получить

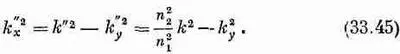
Предположим на мгновение, что n 1 и n 2— вещественные числа (т. е. что мнимая часть показателей очень мала). Тогда все k тоже будут вещественными и из фиг. 33.3 мы видим, что

k y/k =sinq i, k y/k"=sinq t. (33.46)

Но ввиду уравнения (33.44) мы получаем

n 2sinq t =n i sinq i ;, (33.47)

т. е. уже известный нам закон Снелла для преломления. Если же показатель преломления не вещественный, то волновые числа оказываются комплексными и нам следует воспользоваться

(33.45). [Конечно, мы могли бы определить углы q i. и q tиз