Ричард Фейнман - 7. Физика сплошных сред

У подавляющего большинства материалов полный магнитный момент появляется только тогда, когда там присутствуют атомы с незаполненной внутренней электронной оболочкой. Благода­ря этому они могут иметь суммарный момент количества дви­жения и магнитный момент. Такие атомы принадлежат к «пере­ходным элементам» периодической таблицы Менделеева, на­пример: хром, марганец, железо, никель, кобальт, палладий и платина — элементы как раз такого сорта. Кроме того, все редкоземельные элементы имеют незаполненную внутреннюю оболочку, а следовательно, и постоянные магнитные моменты. Правда, встречаются еще странные вещества (к числу их отно­сятся жидкий кислород и окись азота), которые, оказывается, тоже обладают магнитным моментом, но объяснить причины этих странностей я предоставляю химикам.

Предположим теперь, что у нас есть ящик, наполненный молекулами или атомами с постоянным магнитным моментом, скажем газ, жидкость или кристалл. Нам хочется знать, что получится, если мы поместим его во внешнее магнитное поле. В отсутствие магнитного поля атомы сбиваются тепловым движением и их магнитные моменты распределяются по всем направлениям. Но когда действует магнитное поле, оно выстра­ивает эти маленькие магнитики, так что магнитных моментов, направленных по полю, становится больше, чем направленных против него. Материал «намагничивается».

Намагниченность Мматериала мы определяем как полный магнитный момент единицы объема, под которым мы понимаем векторную сумму всех атомных магнитных моментов единицы объема. Если среднее число атомов в единице объема равно N, а их средний момент равен < m> cp, то Мможно записать как про­изведение N на средний магнитный момент:

м= n< m> cp. (35.8)

Это определение Маналогично определению электрической поляризации Р, данному в гл. 10 (вып. 5).

Классическая теория парамагнетизма, как вы уже убедились в гл. 10 (вып. 5), в точности аналогична теории диэлектрической проницаемости. Предполагается, что магнитный момент m каждого из атомов всегда имеет одну и ту же величину, но может быть направлен в любую сторону. Магнитная энергия в поле В равна - m·B=-mBcosq, где q — угол между моментом и полем. Согласно статистической физике, относительная вероят­ность угла равна e - энергия / kTтак что угол 0° более вероятен, чем угол p. Следуя в точности по пути, проделанному нами в гл. 11, § 3 (вып. 5), мы обнаружим, что для слабых магнитных полей Мнаправлена параллельно Ви имеет величину

[См. выражение (11.20), вып. 5.] Эта приближенная формула верна, только когда отношение m B/kT много меньше единицы.

Мы нашли, что намагниченность, т. е. магнитный момент единицы объема, пропорциональна магнитному полю. Это яв­ление и называется парамагнетизмом. Вы увидите, что эффект сильнее проявляется при низких температурах и слабее при высоких. При помещении вещества в магнитное поле возникаю­щий в нем магнитный момент в случае слабых полей пропор­ционален величине поля. Отношение М к В (для слабых полей) называется магнитной восприимчивостью.

Рассмотрим теперь парамагнетизм с точки зрения квантовой механики. Обратимся сначала к атомам со спином 1 / 2 . Если в отсутствие магнитного поля атомы обладают вполне определенной энергией, то в магнитном поле энергия изменится; возможны два значения энергии для разных значений J z. Для J z=+h/2

магнитное поле изменяет энергию на величину

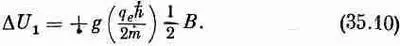
(Для атомов сдвиг энергии DU положителен, ибо заряд элек­трона отрицателен.) Для J г=- h/2 энергия изменяется на величину

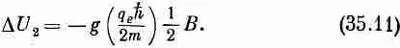
Для сокращения записи обозначим

тогда

DU = ±m 0 В. (35.13)

Совершенно ясен и смысл m 0; — m 0 равно z-компоненте маг­нитного момента для спина, направленного вверх, а + m 0равно z-компоненте магнитного момента в случае спина, на­правленного вниз.

Статистическая механика говорит нам, что вероятность нахождения атома в каком-то состоянии пропорциональна

g - (энергия состояния)/ kT .

В отсутствие магнитного поля энергия обоих состояний одна и та же, поэтому в случае равновесия в магнитном поле ве­роятности пропорциональны

е - D U / kT , (35.14)

Число же атомов в единице объема со спином, направленным вверх, равно

а со спином, направленным вниз,

Постоянная а должна определяться из условия

N вверх+N вниз=N (35.17)

т.е. равна полному числу атомов в единице объема. Таким образом, мы получаем

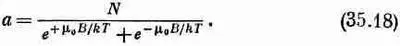
Однако нас интересует средний магнитный момент в на­правлении оси z. Каждый атом со спином, направленным вверх, дает в этот момент вклад, равный -m 0, а со спином, направленным вниз, + m 0, так что средний момент будет

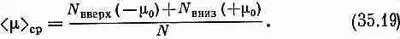
Тогда М — магнитный момент единицы объема — будет равен N ср. Воспользовавшись выражениями (35.15)—(35.17), по­лучим

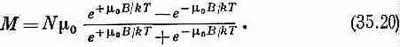
Это и есть квантовомеханическая формула для М в случае атомов со спином j= 1/ 2. К счастью, ее можно записать более коротко через гиперболический тангенс:

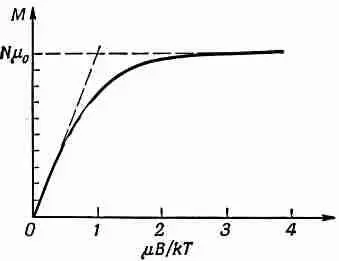
График зависимости М он В приведен на фиг. 35.7.