Ричард Фейнман - 7. Физика сплошных сред

На практике же сигнал на выходе ядерной резонансной аппаратуры не похож на обычную резонансную кривую. Обыч­но это более сложный сигнал с осцилляциями, похожими на те, что изображены на фиг. 35.8. Такая форма сигнала обусловлена изменяющимися полями. Объяснять ее следовало бы с точки зрения квантовой механики, однако можно показать, что объ­яснение таких экспериментов при помощи представлений клас­сической физики, как мы их использовали выше, тоже дает правильный ответ. С точки зрения классической физики мы бы сказали, что когда мы попадаем в резонанс, то синхронно начинаем раскачивать множество прецессирующих ядерных магнитиков. В результате мы их заставляем прецессировать все вместе. А вращаясь все вместе, эти маленькие магнитики создают в катушке индуцированную э.д.с. с частотой, равной w p. Но поскольку со временем магнитное поле увеличивается, то увеличивается и частота прецессии, поэтому наведенное напряжение вскоре приобретает частоту, большую, чем частота генератора. Так как при этом наведенная э.д.с. попеременно попадает то в фазу, то в противофазу с переменным внешним полем, «поглощенная» мощность становится попеременно то положительной, то отрицательной. Таким образом, на экране мы видим запись биений между частотой протона и частотой генератора. Из-за того что частоты не всех протонов в точности одинаковы (разные протоны находятся в нескольких различных полях), а возможно, и в результате возмущений, вносимых атомами железа, находящимися в воде, свободно прецессирующие моменты скоро выбиваются из фазы и сигналы биений исче­зают.

Эти явления магнитного резонанса используются во многих методах как орудие выяснения новых свойств вещества — осо­бенно в химии и в физике. Я не говорю уже о том, что число магнитных моментов ядра говорит нам кое-что и о его структуре. В химии многое можно узнать из структуры (или формы) резонансов. Благодаря магнитным полям, создаваемым близлежа­щими ядрами, точная частота ядерного резонанса для данного частного атома немного сдвигается; величина этого сдвига зависит от окружения, в котором он находится. Измерение этих сдвигов помогает определить, какой атом находится рядом с каким, и проливает свет на детали структуры молекул. Столь же важен и электронный спиновый резонанс свободных ради­калов. Такие радикалы, обычно крайне неустойчивые, часто появляются на промежуточных этапах ряда химических реак­ций. Измерение электронного спинового резонанса служит очень чувствительным индикатором при обнаружении свободных радикалов и часто дает ключ к пониманию механизма некоторых химических реакций.

* Обычные пары натрия в основном моноатомны, хотя изредка там и встречаются молекулы Na 2 .

§ 1. Токи намагничивания

§ 2. Поле Н

§ 3. Кривая намагннчивання

§ 4. Индуктивность с железным сердечником

§ 5. Электромагниты

§ 6. Спонтанная намагниченность

Повторить: гл. 10 (вып. 5)«Диэлектрики»

гл. 17 (вып. 6) «Законы индукции»

§ 1. Токи намагничивания

В этой главе мы поговорим о некоторых материалах, в которых полный эффект магнит­ных моментов проявляется во много раз силь­нее, чем в случае парамагнетизма или диамагне­тизма. Это явление называется ферромагне­тизмом. В парамагнитных и диамагнитных материалах при помещении их во внешнее магнитное поле возникает обычно настолько слабый наведенный индуцированный магнитный момент, что нам не приходится думать о доба­вочных магнитных полях, создаваемых этими магнитными моментами. Другое дело магнит­ные моменты ферромагнитных материалов, ко­торые создаются приложенным магнитным по­лем. Они очень велики и оказывают существен­ное воздействие на сами поля. Эти индуцирован­ные магнитные моменты так огромны, что они вносят главный вклад в наблюдаемые поля. Поэтому нам следует позаботиться о матема­тической теории больших индуцированных маг­нитных моментов. Это, разумеется, чисто фор­мальный вопрос. Физическая проблема состоит в том, почему магнитные моменты столь велики и как они «устроены». Но к этому вопросу мы подойдем немного позже.

Нахождение магнитных полей в ферромаг­нитных материалах несколько напоминает за­дачу о нахождении электрических полей в диэлектриках. Помните, сначала мы описывали внутренние свойства диэлектрика через век­торное поле Р— дипольный момент единицы объема. Затем мы сообразили, что эффект этой поляризации эквивалентен плотности заряда r пол, определяемой дивергенцией Р;

r пол= - С· Р. (36.1)

Полный же заряд в лю­бой ситуации можно запи­сать в виде суммы этого поляризационного заряда и всех других зарядов, плотность которых мы обозначим через r др. Тогда уравнения Максвелла, ко­торые связывают дивергенцию Ес плотностью заря­дов, примут вид:

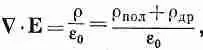
или

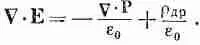
Затем мы можем пере­бросить поляризационную часть заряда в левую сторону уравнения и получить

С· (e 0 Е+ Р)=r др. (36.2)

Этот новый закон говорит, что дивергенция величины (e 0 Е+ Р) равна плотности других зарядов.

Совместная запись Еи Р, как это сделано в уравнении (36.2), полезна, разумеется, только когда мы знаем какие-то соотношения между ними. Мы видели, что теория, связываю­щая наведенный электрический дипольный момент с полем,— вещь довольно сложная и ее на самом деле можно применять только в относительно простых случаях, но и то только как приближение. Я хочу напомнить вам об одном приближении.

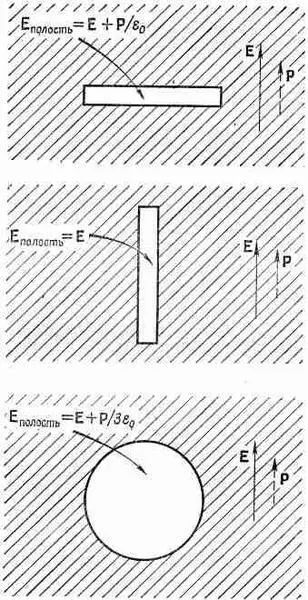
Фиг. 36.1. Электрическое по­ле в полости в диэлектрике за­висит от формы полости.

Чтобы найти наведенный дипольный момент атома внутри диэлектрика, необходимо знать электрическое поле, которое действует на отдельный атом. В свое время мы использовали приближение, пригодное во многих случаях; было предполо­жено, что на атом действует поле, которое было бы в центре небольшой полости, оставшейся после удаления этого атома (считая, что дипольные моменты всех других соседних атомов при этом не изменяются). Вспомните также, что электрическое поле в полости внутри поляризованного диэлектрика зависит от формы этой полости. Эти результаты мы подытожили на фиг. 36.1. В тонкой дискообразной полости, перпендикулярной направлению поляризации, электрическое поле, как было пока­зано с помощью закона Гаусса, имеет вид