Ричард Фейнман - 6a. Электродинамика

Вы понимаете, конечно, что в тот момент, когда получены формулы для потенциалов произвольно движущегося заряда, мы имеем полную электродинамику; из принципа суперпози­ции мы можем получить потенциалы для любого распределения зарядов.

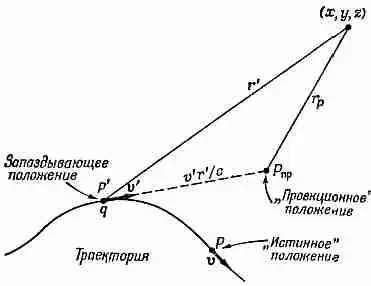
Фиг. 26.2. Движение за­ряда по произвольной тра­ектории.

Потенциалы в точке (х, у, z) в момент t определяются положением Р' и скоростью v' в за­паздывающий момент t'— t-r' /с. Их удобно выражать через коор­динаты относительно «проек­ционного» положения P пр (ис­тинным положением в момент t является точка Р).

Следовательно, все явления электродинамики можно вывести либо из уравнений Максвелла, либо из следующего ряда замечаний. (Запомните их на случай, если вы вдруг очу­титесь на необитаемом острове. Исходя из них, можно восста­новить все. Преобразования Лоренца вы, конечно, помните. Не забывайте их ни на необитаемом острове, ни в каком-либо другом месте.)

Во-первых, А m — четырехвектор. Во-вторых, кулонов по­тенциал любого покоящегося заряда равен q/4pe 0r. В-тре­тьих, потенциал, созданный зарядом, движущимся произволь­ным образом, зависит только от положения в запаздывающий момент времени. Из этих трех фактов вы можете получить все. Из того, что А m ~ четырехвектор, мы преобразованием кулонова потенциала, который известен, получим потенциал за­ряда, движущегося с постоянной скоростью. Затем из послед­него утверждения, что потенциал зависит только от скорости в запаздывающий момент, мы, используя проекционное положе­ние, можем их найти. Правда, это не очень-то удобный способ рассмотрения, но интересно убедиться в том, что законы физики можно сформулировать множеством самых различных способов.

Иногда кое-кто безответственно заявляет, что вся электро­динамика может быть получена только из преобразований Ло­ренца и закона Кулона. Это, конечно, совершенно неверно. Мы прежде всего должны предположить, что у нас имеются скаляр­ный и векторный потенциалы, которые в совокупности образуют четырехвектор. Это говорит нам, как преобразуются потен­циалы. Затем, откуда нам известно, что необходимо учитывать только эффект в запаздывающий момент? Или, еще лучше, по­чему потенциал зависит только от положения и скорости и не зависит, например, от ускорения? Ведь поля Е и В зависят все-таки и от ускорения. Если вы попытаетесь применить те же рассуждения к ним, то будете вынуждены признать, что они за­висят только от положения и скорости в запаздывающий мо­мент. Но тогда поле ускоряющегося заряда было бы таким же, как и поле от заряда в проекционном положении, а это неверно. Поля зависят не только от положения и скорости вдоль траек­тории, но и от ускорения. Так что в «великом» утверждении, что все можно получить из преобразования Лоренца, содержится еще несколько неявных дополнительных предположений. (Всегда, когда вы слышите подобное эффектное утверждение, что нечто большое можно построить на основе малого числа предположений,— ищите ошибку. Обычно неявно принимается довольно много такого, что оказывается далеко не очевидным, " если посмотреть внимательнее.)

§ 2. Поля точечного заряда, движущегося с постоянной скоростью

Итак, мы нашли потенциалы точечного заряда, движущегося с постоянной скоростью. Для практических целей нам нужно найти поля. Равномерно движущиеся заряды попадаются бук­вально на каждом шагу, скажем проходящие через камеру Вильсона космические лучи или даже медленно движущиеся электроны в проводнике. Так что давайте хотя бы посмотрим, как выглядят эти поля для любых скоростей заряда, даже для скоростей, близких к скорости света, но предположим при этом, что ускорение вообще отсутствует. Это очень интересный вопрос.

Поля мы будем находить по обычным правилам, исходя из потенциалов

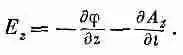
Возьмем сначала E z :

Но компонента A z равна нулю, а дифференцирование выра­жения (26.1) для j дает

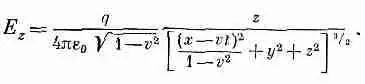
(26.2)

Аналогичная процедура для Е у приводит к

(26.3)

Немного больше работы с x-компонентой. Производная от j более сложна, да и А х не равна нулю. Давайте сначала вычислим — д j /дх:

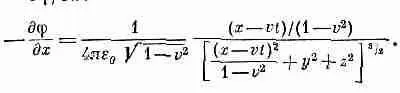
(26.4)

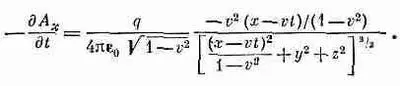
А затем продифференцируем А х по t:

(26.5)

И, наконец, складывая их, получаем

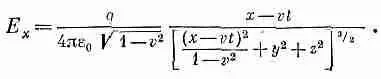
(26.6)

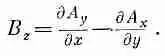
Бросим на минуту заниматься полем Е, а сначала найдем В. Для его z-компоненты мы имеем

Но, поскольку А y равна нулю, у нас остается только одна производная. Заметьте, однако, что А х просто равна vj, а производная (d/dy)v jравна — vE y . Так что

(26.7)

Аналогично,

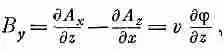
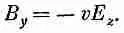
или

(26.8)

Наконец, компонента В х равна нулю, поскольку равны нулю и А у и А г . Таким образом, магнитное поле можно запи­сать в виде

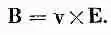
(26.9)

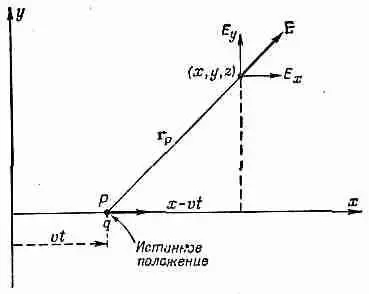
Теперь посмотрим, как выглядят наши поля. Мы попытаемся нарисовать картину поля вокруг положения заряда в настоящий момент. Конечно, влияние заряда в каком-то смысле происхо­дит из запаздывающего положения, но, поскольку мы имеем дело со строго заданным движением, запаздывающее положение однозначно определяется положением в настоящий момент. При постоянной скорости заряда поля лучше связывать с теку­щими координатами, ибо компоненты поля в точке х, у, z за­висят только от (х-vt), у и z, которые являются компонентами вектора перемещения r p из постоянного положения заряда в точку (х, у, z) (фиг. 26.3).