Ричард Фейнман - 6a. Электродинамика

(25.31)

который можно назвать «гауссовой электрической несообраз­ностью». Продолжая этот процесс, вы можете ввести U 3, U 4и т. д. для каждого из физических законов.

Наконец, полной несообразностью мира U вы называете сумму U i,- для каждого из различных явлений, т. е. U=2Ui .

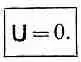
И тогда «великий закон природы» гласит:

(25.32)

Этот «закон», разумеется, утверждает лишь, что сумма квад­ратов всех отдельных отклонений равна нулю, однако един­ственный способ сделать сумму квадратов множества членов равной нулю — это приравнять нулю каждое из ее слагаемых.

Таким образом, «удивительно простой закон» (25.32) экви­валентен целому ряду уравнений, которые вы писали первона­чально. Поэтому совершенно очевидно, что простые обозначе­ния, скрывающие сложности за определением символов,— это еще не истинная простота. Это только трюк. Так и в выражении (25.32) за кажущейся простотой скрывается несколько уравне­ний; это снова не более чем трюк. Развернув их, вы снова полу­чите то, что было раньше.

Однако закон электродинамики, написанный в форме урав­нения (25.29), содержит нечто большее, чем простую запись; в векторном анализе, кроме простоты записи, также есть нечто большее. Тот факт, что уравнения электромагнетизма можно за­писать в особых обозначениях, которые специально приспособ­лены для четырехмерной геометрии преобразований Лоренца, иначе говоря, как векторные уравнения в четырехмерном мире, означает, что они инвариантны относительно преобразований Лоренца. Именно потому, что уравнения Максвелла инвариантны относительно этих преобразований, их можно записать в столь красивом виде.

В том, что законы электродинамики можно записать в форме элегантного уравнения (25.29), нет ничего случайного. Теория относительности была развита именно потому, что эксперимен­тально подтвердилась неизменность предсказанных уравнением Максвелла явлений в любой инерциальной системе. Именно при изучении трансформационных свойств уравнений Максвелла Лоренц открыл свои преобразования как преобразования, ос­тавляющие инвариантными эти уравнения.

Однако есть и другая причина записывать уравнения в та­ком виде. Было обнаружено, что все законы физики должны быть инвариантными относительно преобразований Лоренца (первый об этом догадался Эйнштейн). Таково содержание прин­ципа относительности. Поэтому если вы изобрели обозначения, которые сразу же показывают, инвариантен ли выписанный нами закон, то можно гарантировать, что при попытке соз­дать новую теорию вы будете писать только уравнения, согла­сующиеся с принципом относительности.

В простоте уравнений Максвелла в этих частных обозначе­ниях никакого чуда нет. Обозначения специально были приду­маны именно для них. Самая интересная с физической точки зрения вещь состоит в том, что любой физический закон (будь то распространение мезонных волн, или поведение нейтрино в b-распаде, или что-то другое) должен иметь ту же самую инвариантность относительно тех же преобразований. Так что если ваш звездолет движется с постоянной скоростью, то все законы природы вместе преобразуются так, что никаких новых явлений не возникает. Именно благодаря тому, что принцип относитель­ности является законом природы, уравнения нашего мира в четырехмерных обозначениях должны выглядеть гораздо проще.

*Вас может удивить, почему же мы не пользуемся реакцией

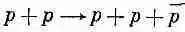
Или даже

для которой, несомненно, требуется меньшая энергия? Все дело в прин­ципе, называемом сохранением барионного заряда, согласно которому вели­чина, равная числу протонов минус число антипротонов, не может изме­ниться. В левой стороне нашей реакции эта величина равна 2. Следова­тельно, если мы хотим справа иметь антипротон, то ему должны сопут­ствовать еще три протона (или других бариона).

* В английском оригинале «unworldliness». — Прим. ред.

§ 1. Четырехмерный потенциал дви­жущегося заряда

§ 2. Поля точечного заряда, движу­щегося с посто­янной скоростью

§ 3. Релятивистское преобразование полей

§ 4. Уравнение движения в релятивистских обозначениях

В этой главе c=1

Повторить: гл. 20 «Решение урав­нений Максвелла в пустом пространстве»

§ 1. Четырехмерный потенциал движущегося заряда

В предыдущей главе мы видели, что потен­циал A m=(j, А) является четырехвектором. Его временной компонентой служит скалярный по­тенциал j, а тремя пространственными компо­нентами— векторный потенциал А. Используя преобразования Лоренца, мы нашли также потенциал частицы, движущейся прямолинейно с постоянной скоростью. (В гл. 21 то же самое было сделано несколько иным методом.) Для точечного заряда, координаты которого в мо­мент t равны (vt, 0, 0), потенциалы в точке (х, у, z) имеют вид

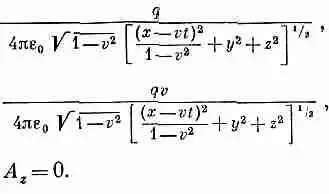
(26.1)

Уравнения (26.1) дают потенциалы в точке х, у, z в момент t, возникающие от движуще­гося заряда, «истинное» положение которого (имеется в виду положение в момент времени t) x=vt. Заметьте, что в уравнение входят координаты (x-vt), у и z, которые являются коор­динатами относительно переменного положения Р движущегося заряда (фиг. 26.1). Но, как вы знаете, истинное влияние распространяется на самом деле со скоростью с, так что поле в точке определяется на самом деле запаздывающим положением заряда Р', координата х которого равна vt' (где t'=t-r'/с — «запаздывающее» время».)

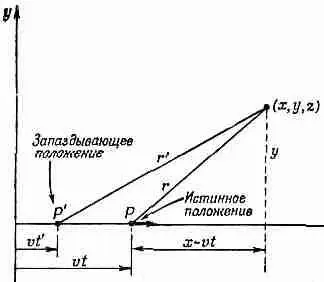
Фиг. 26.1. Определение полей в точке P от заряда q, движущегося вдоль оси x с постоянной скоростью v. (Поле в точке (x, y, z) в «настоящий момент» можно выразить как через «истинное» положение P так и через «запаздывающее» положение P’ (т. е. положение в момент t’=t-r’/c).

Нам, однако, известно, что заряд двигался с постоянной скоростью по прямой линии, поэтому естественно, что поведение в точке Р' непосредственно связано с переменным положением заряда. Фактически, если мы добавим предположение, что потен­циалы зависят только от положения и скорости в запаздывающий момент, тогда уравнение (26.1) будет представлять собой полную формулу для потенциалов заряда, движущегося любым обра­зом. Вот как все это работает. Пусть у вас имеется заряд, дви­жущийся каким-то произвольным образом, скажем, по траекто­рии, изображенной на фиг. 26.2, и вы пытаетесь найти потен­циал в точке (х, у, z ). Прежде всего вы находите запаздывающее положение Р' и скорость v ' в этой точке. Вообразите затем, что заряд сохраняет свое движение с этой скоростью на весь период запаздывания (t'-t), так что он появился бы затем в воображае­мом положении Р пр, которое мы будем называть «проекци­онным», причем двигаясь с той же скоростью v'. (На самом деле он, конечно, не делает этого; в момент t он находится в точке Р.) Тогда потенциалы в точке (х, у, z) будут как раз такими, кото­рые дали бы уравнения (26.1) для воображаемого заряда в про­екционном положении Р пр. Мы хотим здесь сказать, что, по­скольку потенциалы зависят только от того, что делает заряд в запаздывающий момент, они будут одинаковы, независимо от того, продолжает ли заряд свое движение с постоянной скоро­стью или изменяет его после момента t' , т. е. после того, как по­тенциалы, которые возникнут в момент t в точке (х, у, z ), уже определены.