Ричард Фейнман - 5a. Электричество и магнетизм
- Название:5a. Электричество и магнетизм
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Ричард Фейнман - 5a. Электричество и магнетизм краткое содержание
5a. Электричество и магнетизм - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
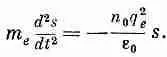
(7.23)
Отсюда следует, что s меняется по гармоническому закону. Во времени s меняется как cos wt или, если использовать экспоненту (см. вып. 3), как
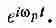
(7.24)
Частота колебаний w р определяется из (7.23):
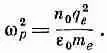
(7.25)
Это число, характеризующее плазму, называют собственной частотой колебаний плазмы, или плазменной частотой.
Оперируя с электронами, многие предпочитают получать ответы в единицах e 2 , определяемых как

(7.26)
При этом условии (7.25) превращается в
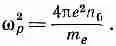
(7.27)
В таком виде эту формулу можно встретить во многих книгах.
Итак, мы обнаружили, что возмущения плазмы приводят к свободным колебаниям электронов вблизи положения равновесия с собственной частотой w р , пропорциональной корню квадратному из плотности электронов. Плазменные электроны ведут себя как резонансная система, подобная описанным в вып. 2, гл. 23.
Этот собственный резонанс плазмы приводит к интересным эффектам. Например, при прохождении радиоволн сквозь ионосферу обнаруживается, что они могут пройти только в том случае, если их частота выше плазменной частоты. А иначе они отражаются обратно. Для связи с искусственным спутником мы используем высокие частоты. Если же мы хотим связаться с радиостанцией, расположенной где-то за горизонтом, то необходимы частоты меньшие, чем плазменная частота, иначе сигнал не отразится обратно к Земле.
Другой интересный пример колебаний плазмы наблюдается в металлах. В них содержится плазма из положительных ионов и свободных электронов. Плотность n 0 там очень высока, значит, велика и w р . Но колебания электронов все же можно обнаружить. Ведь, согласно квантовой механике, гармонический осциллятор с собственной частотой w р обладает уровнями энергии, отличающимися друг от друга на величину h w р. Значит, если, скажем, обстреливать электронами алюминиевую фольгу и очень точно измерять их энергию по ту сторону фольги, то можно ожидать, что временами электроны будут из-за колебаний плазмы терять как раз энергию hw p . Так это и происходит. Впервые это явление наблюдалось экспериментально в 1936 г. Электроны с энергиями от нескольких сот до нескольких тысяч электронвольт, рассеиваясь от тонкой металлической фольги или проходя сквозь нее, теряли энергию порциями. Эффект оставался непонятым до 1953 г., пока Бом и Пайнс не показали, что все это можно объяснить квантовым возбуждением плазмы в металле.
§ 4. Коллоидные частицы в электролите
Обратимся к другому явлению, когда местоположение зарядов определяется потенциалом, создаваемым в какой-то степени самими зарядами. Такой эффект существен для поведения коллоидов. Коллоид — это взвесь маленьких заряженных частичек в воде. Хотя эти частички и микроскопические, но по сравнению с атомом они все же очень велики. Если бы коллоидные частицы не были заряжены, они бы стремились коагулировать (слиться) в большие комки; но, будучи заряженными, они отталкиваются друг от друга и остаются во взвешенном состоянии. Если в воде растворена еще соль, то она диссоциирует (расползается) на положительные и отрицательные ионы. (Такой раствор ионов называется электролитом.) Отрицательные ионы притягиваются к коллоидным частицам (будем считать, что их заряды положительны), а положительные — отталкиваются. Нам нужно узнать, как ионы, окружающие каждую частицу коллоида, распределены в пространстве.
Чтобы мысль была яснее, рассмотрим только одномерный случай. Представим себе коллоидную частицу в виде очень большого (по сравнению с атомом!) шара; тогда мы можем малую часть ее поверхности считать плоскостью. (Вообще, пытаясь понять новое явление, лучше разобраться в нем на чрезвычайно упрощенной модели; и только потом, поняв суть проблемы, стоит браться за более точные расчеты.)
Предположим, что распределение ионов создает плотность зарядов р(х) и электрический потенциал j, связанные электростатическим законом С 2j =-r/e 0, или в одномерном случае законом
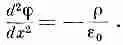
(7.28)
Как бы распределились ионы в таком поле, если бы потенциал подчинялся этому уравнению? Узнать это можно при помощи принципов статистической механики. Вопрос в том, как определить j, чтобы вытекающая из статистической механики плотность заряда тоже удовлетворяла бы условию (7.28)?
Согласно статистической механике (см. вып. 4, гл. 40), частицы, пребывая в тепловом равновесии в поле сил, распределяются так, что плотность n частиц с координатой x дается формулой
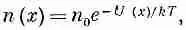
(7.29)
где U(x) — потенциальная энергия, k — постоянная Больцмана, а Т — абсолютная температура.
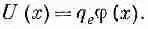
Предположим, что у всех ионов один и тот же электрический заряд, положительный или отрицательный. На расстоянии х от поверхности коллоидной частицы положительный ион будет обладать потенциальной энергией
Плотность положительных ионов тогда равна
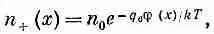
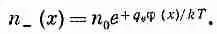
а плотность отрицательных
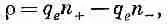
Суммарная плотность заряда
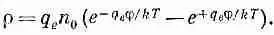
или
(7.30)
Подставляя в (7.28), увидим, что потенциал j должен удовлетворять уравнению
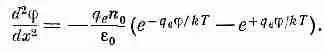
(7.31)
Это уравнение решается в общем виде [помножьте обе его части на 2(dj/dx)и проинтегрируйте по х],но, продолжая упрощать задачу, мы ограничимся здесь только предельным случаем малых потенциалов или высоких температур Т. Малость j отвечает разбавленному раствору. Показатель экспоненты тогда мал, и можно взять
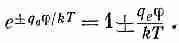
Интервал:
Закладка:





