Ричард Фейнман - 5a. Электричество и магнетизм

Взяв V из (8.8), напишем

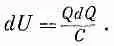
Или, интегрируя от Q=0 до конечного заряда Q, получаем

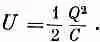
(8.9)

Эту энергию можно также записать в виде

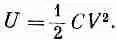
(8.10)

Вспоминая, что емкость проводящей сферы (по отношению к бесконечности) равна

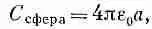
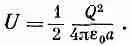
мы немедленно получим из уравнения (8.9) энергию заряженной сферы

(8.11)

Это выражение, конечно, относится также и к энергии тонкого сферического слоя с полным зарядом Q; получается 5/ 6энер­гии однородно заряженного шара [уравнение (8.7)].

Посмотрим, как применяется понятие электростатической энергии. Рассмотрим два вопроса. Какова сила, действующая между обкладками конденсатора? Какой вращательный (крутя­щий) момент вокруг некоторой оси испытывает заряженный про­водник в присутствии другого проводника с противоположным зарядом? На такие вопросы легко ответить, пользуясь нашим выражением (8.9) для электростатической энергии конденсатора и принципом виртуальной работы (см. вып. 1, гл. 4, 13 и 14).

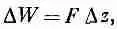
Применим этот метод для определения силы, действующей между двумя обкладками плоского конденсатора. Если мы пред­ставим, что промежуток между пластинами расширился на не­большую величину Dz, то тогда механическая работа, произво­димая извне для того, чтобы раздвинуть обкладки, была бы равна

(8.12)

где F — сила, действующая между обкладками. Эта работа обя­зана быть равной изменению электростатической энергии кон­денсатора, если только заряд конденсатора не изменился.

Согласно уравнению (8.9), энергия конденсатора первона­чально была равна

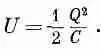
Изменение в энергии (если мы не допускаем изменения величи­ны заряда) тогда равно

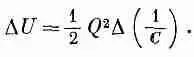
(8.13)

Приравнивая (8.12) и (8.13), получаем

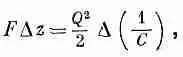
(8.14)

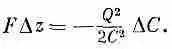
что может также быть записано в виде

(8.15)

Ясно, эта сила здесь возникает от притяжения зарядов на обкладках; мы видим, однако, что заботиться о том, как там они рас­пределены, нам нечего; единственное, что нам нужно, — это учесть емкость С.

Легко понять, как обобщить эту идею на проводники произ­вольной формы и на прочие составляющие силы. Заменим в урав­нении (8.14) F той составляющей, которая нас интересует, а Dz — малым смещением в соответствующем направлении. Или если у нас есть электрод, насаженный на какую-то ось, и мы хо­тим знать вращательный момент t, то запишем виртуальную ра­боту в виде

DW = tDq,

где Dq — небольшой угловой поворот. Конечно, теперь D(1/C) должно быть изменением 1/С, отвечающим повороту на Dq.

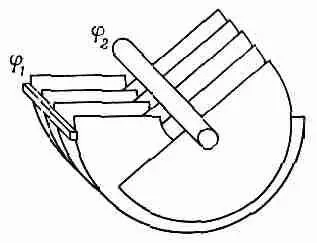
Фиг. 8.3. Чему равен вращатель­ный момент, действующий на переменный конденсатор?

Таким способом мы можем определить вращательный момент, действующий на подвижные пластины переменного конденса­тора, показанного на фиг. 8.3.

Вернемся к частному случаю плоского конденсатора; мы можем взять формулу для емкости, выведенную в гл. 6:

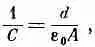
(8.16)

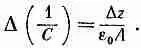
где А— площадь каждой обкладки. Если промежуток уве­личится на Dz, то

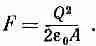
Из (8.14) тогда следует, что сила притяжения между двумя обкладками равна

(8.17)

Взглянем на уравнение (8.17) повнимательнее и подумаем, нельзя ли сказать, как возникает эта сила. Если заряд на одной из обкладок мы запишем в виде

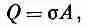
то (8.17) можно будет переписать так:

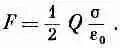
Или поскольку поле между пластинами равно

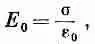
то

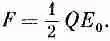
(8.18)

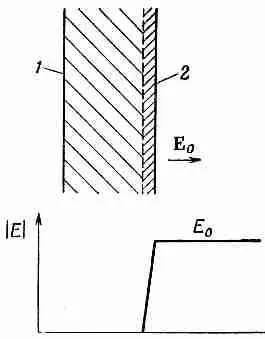
Можно было сразу догадаться, что сила, действующая на одну из пластин, будет равна заряду Q этой пластины, умножен­ному на поле, действующее на заряд. Но что удивляет, так это множитель 1/ 2. Дело в том, что Е 0 — это не то поле, которое действует на заряды. Если вообразить, что заряд на поверх­ности пластины занимает какой-то тонкий слой (фиг. 8.4), то поле будет меняться от нуля на внутренней границе слоя до Е 0 в пространстве снаружи пластин. Среднее поле, действующее на поверхностные заряды, равно Е 0 /2. Вот отчего в (8.18) стоит множитель 1/ 2.

Вы должны обратить внимание на то, что, рассчитывая вир­туальную работу, мы предположили, что заряд конденсатора постоянен, что конденсатор не был электрически связан с дру­гими предметами и полный заряд не мог изменяться.

Фиг. 8.4. Поле у поверхности проводника меняется от нуля до E 0=s/e 0, когда пересечен слой по­верхностного заряда. 1 — проводящая пластина; 2 — слой поверхностного заряда.

А теперь пусть мы предположили, что при виртуальных пе­ремещениях конденсатор поддерживается при постоянной раз­ности потенциалов. Тогда мы должны были бы взять

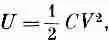
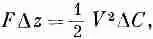
и вместо (8.15) мы бы имели

что приводит к силе, равной по величине той, что была получена в уравнении (8.15) (так как V = Q/C), но с противоположным знаком!

Конечно, сила, действующая между пластинами конденса­тора, не меняет свой знак, когда мы отсоединяем конденсатор от источника электричества. Кроме того, мы знаем, что две плас­тины с разноименными электрическими зарядами должны при­тягиваться. Принцип виртуальной работы во втором случае был применен неправильно, мы не приняли во внимание виртуаль­ную работу, производимую источником, заряжающим конден­сатор. Это значит, что для того, чтобы удержать потенциал при постоянном значении V, когда меняется емкость, источник элект­ричества должен снабдить конденсатор зарядом VDC. Но этот заряд поступает при потенциале V, так что работа, выполняе­мая электрической системой, удерживающей заряд постоянным, равна V 2DC. Механическая работа .FDz плюс эта электрическая работа V 2DC вместе приводят к изменению полной энергии кон­денсатора на 1/ 2V 2DC. Поэтому на механическую работу, как и прежде, приходится F D z=- 1 / 2 V 2DC.