Ричард Фейнман - 4a. Кинетика. Теплота. Звук

Теперь мы можем показать (наконец-то!), что скорость рас­пространения рентгеновских лучей в куске угля, например, не больше, чем скорость света, хотя фазовая скорость больше скорости света. Чтобы сделать это, нужно найти соотношение dw/dk, которое мы вычислим дифференцированием формулы

(48.14): dk/dw=1/c+a/(w 2 c). А групповая скорость равна обрат­ной величине, т. е.

что меньше, чем с! Таким образом, хотя фазы могут бежать бы­стрее скорости света, модулирующие сигналы движутся мед­леннее, и в этом состоит разрешение кажущегося парадокса!

Разумеется, в простейшем случае w=kc групповая скорость d w /dk тоже равна с, т. е. когда все фазы движутся с одинако­вой скоростью, естественно, и групповая скорость будет той же самой.

§ 5. Амплитуда вероятности частиц

Рассмотрим еще один необычайно интересный пример фа­зовой скорости. Он относится к области квантовой механики. Известно, что амплитуда вероятности найти частицу в данном месте изменяется при некоторых обстоятельствах в пространстве и времени (давайте возьмем одно измерение) следующим обра­зом:

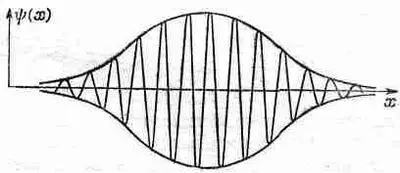
где w — частота, связанная с классической энергией, E=h w , a k — волновое число, которое связано с импульсом соотно­шением р=hk. Мы говорим, что частица имеет определенный импульс р, если волновое число в точности равно k, т. е. если бежит идеальная волна повсюду с одинаковой амплитудой. Выражение (48.19) дает амплитуду вероятности, но если мы возьмем квадрат абсолютной величины, то получим относитель­ную вероятность обнаружения частицы как функцию поло­жения и времени. В данном случае она равна постоянной, что означает вероятность обнаружить частицу в любом месте, Рассмотрим теперь такой случай, когда известно, что обна­ружить частицу в каком-то месте более вероятно, чем в других местах. Подобную картину мы описываем волной, которая имеет максимум в данном месте и сходит на нет по мере удале­ния в стороны (фиг. 48.6).

Фиг. 48.6. Локализованный волновой пакет,

(Это не то же самое, что изображено на фиг. 48.1, где волна имеет целый ряд максимумов, но сними вполне можно расправиться, сложив несколько волн с при­близительно одинаковыми значениями w и k. Таким способом можно избавиться от всех максимумов, кроме одного.)

При этих обстоятельствах, поскольку квадрат выражения (48.19) представляет вероятность найти частицу в некотором месте, мы знаем, что в данный момент больше шансов найти ча­стицу вблизи центра «колокола», где амплитуда максимальна.

Если подождать немного, то волна передвинется, и по проше­ствии некоторого промежутка времени «колокол» перейдет в какое-то другое место. Зная, что частица вначале где-то была расположена, мы ожидали бы, согласно классической меха­нике, что она будет где-то и позднее, ведь есть же у нее ско­рость и импульс в конце концов. При этом квантовая теория дает в пределе правильные классические соотношения между энергией, импульсом и скоростью, если только групповая ско­рость, скорость модуляции, будет равна скорости классиче­ской частицы с тем же самым импульсом.

Сейчас необходимо показать, так ли это на самом деле или нет. Согласно классической теории, энергия связана со ско­ростью уравнением

Точно таким же образом импульс равен

Как следствие отсюда после исключения v получается

E 2-р 2c 2=m 2c 4,

т. е. р m р m =m 2 . Это величайший результат четырехмерья, о котором мы уже говорили много раз, устанавливающий связь между энергией и импульсом в классической теории. Теперь же, поскольку мы собираемся заменить E и p на w и k помощью подстановки Е=h wи p=hk, он означает, что в квантовой меха­нике должна существовать связь

Таким образом, возникло соотношение между частотой и вол­новым числом квантовомеханической амплитуды, описывающей частицу с массой m. Из этого уравнения можно получить

т. е. фазовая скорость w/k; снова больше скорости света!

Рассмотрим теперь групповую скорость. Она должна быть равна скорости, с которой движется модуляция, т. е. d w/ dk.

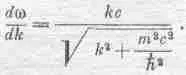
Чтобы найти ее, нужно продифференцировать квадратный корень; это дело нехитрое. Производная равна

Но входящий сюда квадратный корень есть попросту w /с, так что эту формулу можно записать в виде dw/dk=е 2k/w. Далее, так как k/w равно р/Е, то

Но, согласно (48.20) и (48.21), с 2 р/Е равно v — скорости ча­стицы в классической механике. Таким образом видно, что, принимая во внимание основные квантовомеханические соот­ношения E=h wи p=hk, определяющие w и k через классиче­ские величины Е и р и дающие только уравнение w 2-k 2c 2= =m 2с 4/h 2, теперь можно понять также соотношения (48.20) и (48.21), связывающие Е и р соскоростью. Групповая скорость, разумеется, должна быть скоростью частиц, если эта интер­претация вообще имеет какой-либо смысл. Пусть в какой-то момент, как мы полагаем, частица находится в одном месте, а затем; скажем через 10 минут,— в другом. Тогда, согласно кван­товой механике, расстояние, пройденное «колоколом», разде­ленное на интервал времени, должно равняться классической скорости частицы.

§ 6. Волны в пространстве трех измерений

Мы заканчиваем наше обсуждение волн несколькими об­щими замечаниями о волновом уравнении. Эти замечания, при­званные дать нам картину того, чем нам предстоит заниматься в будущем, вовсе не претендуют на то, чтобы вы поняли их сразу; они должны скорее показать, как будут выглядеть все эти вещи, когда вы несколько больше познакомитесь с волна­ми. Мы уже записали уравнение для распространения звука в одном измерении: