Ричард Фейнман - 4a. Кинетика. Теплота. Звук

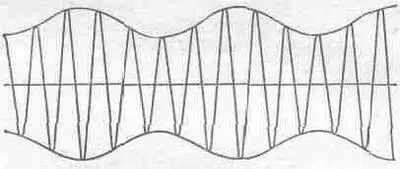
Возьмем простейший с точки зрения математики случай, когда певица берет безупречную ноту с безупречным синусои­дальным колебанием голосовых связок, причем получается сигнал, сила которого меняется, как это показано на фиг. 48.4.

Фиг. 48.4. Модуляция несущей волны. На этом схематическом ри­сунке отношение w c /w m =5. В настоящей радиоволне w c /w m »100.

Изменения слышимой частоты принимаются затем приемником; мы избавляемся от несущей волны и смотрим просто на «оберт­ку», которая представляет собой колебания голосовых связок, или звук голоса певицы. Громкоговоритель же производит колебания той же частоты в воздухе, и в принципе слушатель не может обнаружить разницы между настоящим голосом пе­вицы и передачей, слышимой по радио. В действительности же из-за некоторых искажений и других тончайших эффектов можно все же определить, слышим ли мы радио или «живой» голос певицы; в других же отношениях все происходит так, как мы описали.

§ 3. Боковые полосы

Описанную выше модулированную волну математически можно записать в виде

S=(1+bcosw m t)cosw c t, (48.9)

где (w с — несущая частота, а w m— частота слышимого звука. Используя теоремы о косинусах или свойства экспоненты exp(iq) (разницы в этом никакой нет, однако легче работать с экспонентой), мы получаем

S= cosw ct+ 1/ 2 b cos(w c+w m) t+ 1 / 2 bcos( w с - w m )t. (48.10)

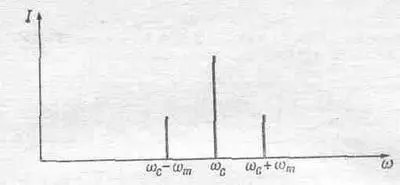
Таким образом, с другой точки зрения можно сказать, что вы­ходящая волна состоит из суперпозиции трех волн: обычной волны с частотой w с, т. е. несущей частоты, и затем двух новых волн с двумя другими частотами. Одна из них равна сумме несущей и модулирующей частот, а другая — разности. Если построить нечто вроде графика зависимости интенсивности излучения генератора от частоты, то сначала мы, естественно, обнаружим большую интенсивность при несущей частоте w с , но как только певица начнет петь, мы неожиданно обнаружим интенсивность, пропорциональную силе голоса певицы b 2 при частотах w с + w mи w с-w m, как это показано на фиг. 48.5.

Фиг. 48.5. Спектр частот несущей волны w с, модулированной одной косинусообразной волной w m .

Они называются боковыми полосами. Если из передатчика вы­ходит модулированный сигнал, то возникают боковые полосы. Если в одно и то же время передаются две ноты, скажем, с частотами w mи w m ', например играют два инструмента или какая-то другая усложненная волна, тогда из математики вид­но, что получаются две новые волны, соответствующие часто­там (w m±w m '.

Итак, если происходит какая-то сложная модуляция, ко­торую можно представить в виде суммы многих косинусов, то оказывается, что в действительности передатчик работает в целой области частот, именно несущей частоты плюс-минус максимальная частота, содержащаяся в модулирующем сиг­нале.

Хотя вначале мы могли поверить, что радиопередатчик ра­ботает только на номинальной несущей частоте, так как в нем находится большой сверхстабильный кристаллический осцил­лятор и все подобрано так, чтобы частота была равна в точности 800 кгц, но в тот момент, когда диктор объявляет, что станция работает на частоте 800 кгц, он тем самым модулирует эту ча­стоту и передача уже не идет точно на этой частоте. Предполо­жим, что усилители построены так, что они могут передавать широкую полосу частот в области, воспринимаемой ухом (ухо может слышать частоты вплоть до 20 000 гц, но обычно радио­приемники и радиопередатчики работают ниже частоты 10 000 гц, и по радио мы высших частот не слышим). Так что голос диктора, объявляющего что-то по радио, может содер­жать частоты вплоть до 10 000 гц, передатчик излучает ча­стоты в области от 790 до 810 кгц. Если при этом на частоте, скажем, 795 кгц работает еще одна радиостанция, то возникают большие помехи. Если мы сделаем наш приемник столь чув­ствительным, что он будет принимать только частоту 800 кгц и не будет захватывать по 10 кгц с каждой стороны, то мы не услышим, что сказал диктор, ведь информация передается именно на боковых частотах! Поэтому очень важно, чтобы стан­ции были разделены некоторой областью частот и их боковые полосы не перекрывались, а приемник не должен быть столь избирательным, чтобы не позволять принимать боковые полосы вместе с номинальной частотой. Но эта проблема не вызывает больших затруднений при радиопередачах. Мы слышим в области ±20 кгц, а радиопередача ведется обычно в области от 500 до 1500 кгц, так что места должно хватить для множества станций.

Проблема телевидения намного труднее. Когда электрон­ный луч бежит по экрану телевизионной трубки, он создает множество светлых и темных точек. Эти светлые и темные точки и есть «сигналы». Обычно, чтобы «показать» весь кадр, лучу требуется примерно в тридцатую долю секунды пробежать 500 строк. Пусть разрешение по горизонтали и по вертикали более или менее одинаково, т. е. на миллиметр каждой строки приходится ровно столько же точек, сколько строк приходится на миллиметр высоты. Нужно, чтобы мы могли различать по­следовательность светлое — темное, светлое — темное, светлое — темное на протяжении 500 линий. Чтобы это можно было сделать с помощью косинусообразной волны, требуется длина волны, т. е. расстояние от максимума до минимума, соответ­ствующая длине 1/250 части экрана. Таким образом, получается 250x500x30 «единичек информации» в секунду, поэтому выс­шая частота, которую нужно передать, оказывается равной приблизительно 4 Мгц. На самом деле, чтобы отделить телеви­зионные станции одну от другой, мы должны использовать несколько большую ширину — около 6 Мгц. Часть ее исполь­зуется для передачи звукового сопровождения и другой инфор­мации. Таким образом, телевизионный канал имеет ширину 6 Мгц. Разумеется, модулировать с частотой, превышающей частоту несущей волны, невозможно, поэтому телевизионные передачи нельзя вести на частоте, например, 800 кгц.

Во всяком случае, телевизионная полоса начинается с частоты 54 Мгц. Первый телевизионный канал в Соединенных Штатах работает в полосе от 54 до 60 Мгц, т. е. имеет ширину 6 Мгц . «Постойте,— можете сказать вы,— ведь только сейчас мы до­казали, что боковые полосы должны быть с обеих сторон, а поэтому ширина должна быть вдвое больше». Оказывается, радиоинженеры довольно хитрый народ. Если при анализе модулирующего сигнала использовать не только косинус, а косинус и синус, чтобы учесть разность фаз, то между высоко­частотной и низкочастотной боковыми полосами обнаружится наличие определенного постоянного соотношения. Этим мы хотим сказать, что вторая боковая полоса не содержит никакой новой информации по сравнению с первой, так что одну из них вполне можно выкинуть. Приемник же устроен таким образом, что потерянная информация восстанавливается из несущей ча­стоты и одной боковой полосы. Передача с помощью одной бо­ковой полосы — очень интересный метод уменьшения ширины полосы, необходимой для передачи информации.