Ричард Фейнман - 4a. Кинетика. Теплота. Звук

здесь с — скорость того, что мы назвали волнами. Если речь идет о звуке, то это скорость звука, если о свете — то это ско­рость света. Мы показали, что для звуковой волны перемещения частиц должны распространяться с некоторой скоростью. Но из­быточное давление, как и избыточная плотность, тоже распро­страняется с некоторой скоростью. Таким образом, можно ожидать, что и давление будет удовлетворять этому же уравнению.

Так оно и есть на самом деле, однако докажите это самостоя­тельно. Указание: r u пропорционально скорости изменения c с расстоянием х. Следовательно, продифференцировав волновое уравнение по х, мы немедленно обнаружим, что д c /дх удовлет­воряет тому же самому уравнению. Другими словами, r uудов­летворяет тому же самому уравнению. Но Р u пропорционально r u, поэтому и Р u удовлетворяет тому же самому уравнению. Та­ким образом, и давление, и перемещение — все описывается одним и тем же уравнением.

Обычно волновое уравнение для звука записывается через давление, а не через перемещение. Это проще, потому что давление — скаляр и не имеет никакого направления. Но перемещение есть вектор, и поэтому лучше иметь дело с дав­лением.

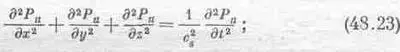
Следующий вопрос, который нам предстоит обсудить, отно­сится к волновому уравнению в трехмерном пространстве. Мы знаем, что звуковая волна в одномерном пространстве описы­вается решением ехр[i(wt- kx)], где w=kc S. Кроме того, нам из­вестно, что в трех измерениях волна описывается выражением exp[i(wt- k x x-k y y-k z z)], и в этом случае w 2=k 2с S 2[сокращен­ная запись (k 2 x+k 2 y+k 2 z)c 2 S]. Сейчас мы хотим просто угадать вид волнового уравнения в трехмерном пространстве. Естествен­но, что в случае звука это уравнение можно получить с помощью тех же самых динамических соображений, но уже в трехмерном пространстве. Однако мы не будем сейчас делать этого, а просто напишем ответ: уравнение для давления или перемещения (или чего-то другого) имеет вид

правильность этого уравнения может быть легко проверена подстановкой в него функции exp[i(wt- k· r)]. Ясно, что при каждом дифференцировании по х происходит умножение на - ik x . Если мы дифференцируем дважды, то это эквивалентно умножению на - k 2 x , так что для такой волны первый член получится равным - k 2 x P u . Точно таким же образом второй член окажется равным -k 2 у Р u , а третий — равным - k 2 z P u . С правой же стороны мы получим -w 2/c 2 SР u. Если мы вынесем 1 за скобку Р и и изменим знаки всех членов, то увидим, что между k и w как раз получится желаемое соотношение.

Возвращаясь назад, мы должны прийти к основному урав­нению, соответствующему дисперсионному соотношению (48.22) для квантовомеханической волны. Если j — амплитуда нахождения частицы в момент t в точке с координатами х, у и z, то основное уравнение квантовой механики для свободной частицы имеет вид

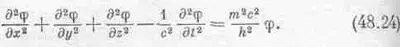
Прежде всего заметим, что релятивистский характер этого уравнения гарантируется появлением координат x, y, z и вре­мени t в такой удачной комбинации, что она автоматически учитывает принцип относительности. Кроме того, это уравне­ние волновое. Если подставить в него плоскую волну, то как следствие мы получим равенство -k 2+w 2/c 2=m 2c 2/h 2, которое должно выполняться в квантовой механике. В этом волновом уравнении содержится еще одна фундаментальная вещь: любая суперпозиция волн также будет его решением. Таким образом, это уравнение опирается на всю квантовую механику и всю теорию относительности, которая уже обсуждалась нами до сих пор, по крайней мере когда мы имели дело с единственной частицей в пустом пространстве без всяких потенциалов и воздействующих на нее сил!

§ 7. Собственные колебания

Вернемся теперь к другим очень любопытным примерам биений, которые немного отличаются от того, что мы рассмат­ривали до сих пор. Представьте себе два одинаковых маятника, которые связаны между собой слабой пружинкой. Длины их должны быть одинаковыми с возможно большей точностью. Если мы оттянем один маятник и отпустим его, то он будет качаться взад и вперед и будет тянуть то взад, то вперед связывающую пружинку, т. е. получится устройство, создающее силу с собственной частотой второго маятника. Можно заключить из знако­мой нам теории резонансов, что если к какому-то предмету при­кладывать с надлежащей частотой силу, то она будет двигать этот предмет. Таким образом, ясно, что один маятник, двигаясь взад и вперед, будет раскачивать второй. Однако при этих усло­виях происходит некое новое явление, связанное с тем, что энергия системы конечна. Первый маятник постепенно рас­трачивает свою энергию, вызывая движение другого маятника, и в конце концов полностью отдаст свою энергию и остано­вится. Вся энергия теперь будет сосредоточена во втором маятнике. Но пройдет немного времени и все будет происхо­дить наоборот: энергия из второго маятника будет перекачи­ваться назад, в первый маятник. Это очень интересное и за­нимательное явление. Мы сказали, что оно связано с теорией биений, и сейчас мы должны показать, как можно понять это явление с точки зрения этой теории.

Обратите внимание, что движение каждого из двух маятни­ков — это колебания с циклически изменяющейся амплитудой. Поэтому движение одного из маятников можно, очевидно, рас­сматривать с различных точек зрения, в частности как сумму двух одновременных колебаний с мало отличающимися часто­тами. Таким образом должно быть возможно обнаружить в этой системе два других движения и утверждать, что поскольку система наша, безусловно, линейная, то мы видим суперпози­цию этих двух решений. Действительно, легко найти два спо­соба так запустить нашу систему, что каждый из них даст в результате идеальное абсолютно периодическое колебание с одной частотой. Движение, с которого мы начали, не строго периодично, оно не продолжается все время (один маятник по­степенно передает свою энергию другому и изменяет свою ам­плитуду), но есть способы так начать движение, что не будет никаких подобных изменений. Как только вы узнаете, что это за способы, то сразу же поймете почему. Если, например, мы запустим оба маятника одновременно, то, поскольку длина их одинакова и пружинка в этом случае бездействует, оба маятника так и будут продолжать качаться все время вместе. (Разумеется, если нет трения и все достаточно хорошо подог­нано.) С другой стороны, существует еще одна возможность создать строго периодическое движение, которое также имеет определенную частоту,— когда маятники, оттянутые вначале в разные стороны на точно равные расстояния, движутся в противоположных направлениях. Нетрудно сообразить, что пружинка немного увеличивает «восстанавливающую силу», возникающую из-за действия силы тяжести, и система колеб­лется с несколько большей частотой, чем в первом случае,— вот и все. Почему с большей? Да потому что пружинка тянет, помогая силе тяжести, и это делает систему более «жесткой», так что частота такого колебания чуть-чуть больше.