Ричард Фейнман - 2a. Пространство. Время. Движение

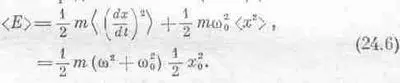
Интересно разобраться также в том, много ли энергии может накопить осциллятор. Не путайте этого вопроса с вопросом о средней мощности, ибо хотя выделяемая силой мощность сна­чала действительно накапливается осциллятором, потом на его долю остается лишь то, что не поглотило трение. В каждый мо­мент осциллятор обладает вполне определенной энергией, по­этому можно вычислить среднюю запасенную энергию . Мы уже вычислили среднее значение (dx/dt) 2 , так что

Если осциллятор достаточно добротен и частота w близка к w 0, то Ѕ х Ѕ — большая величина, запасенная энергия очень велика и можно накопить очень много энергии за счет небольшой силы. Сила производит большую работу, заставляя осциллятор рас­качиваться, но после того, как установилось равновесие, вся сила уходит на борьбу с трением. Осциллятор располагает большой энергией, если трение очень мало, и потери энергии невелики даже при очень большом размахе колебаний. Доб­ротность осциллятора можно измерять величиной запасенной энергии по сравнению с работой, совершенной силой за период колебания.

Что это за величина — накопленная энергия по сравнению с работой силы за цикл? Ее обозначили буквой Q. Величина Q — это умноженное на 2p отношение средней запасенной энер­гии к работе силы за один цикл (можно рассматривать работу не за цикл, а за радиан, тогда в определении Q исчезнет 2p)

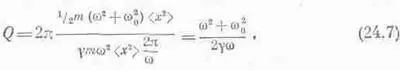
Пока Q не слишком велика — это плохая характеристика системы, если же Q довольно большая величина, то можно сказать, что это мера добротности осциллятора. Многие пыта­лись дать самое простое и полезное определение Q; разные оп­ределения немногим отличаются друг от друга, но если Q очень велика, то все они согласуются друг с другом. При самом общем определении по формуле (24.7) Q зависит от w. Если мы имеем дело с хорошим осциллятором вблизи резонансной частоты, то (24.7) можно упростить, положив w = w 0, тогда Q= w 0 /g, такое определение Q было дано в предыдущей главе. Что такое Q для электрической цепи? Чтобы найти эту ве­личину, надо заменить m на L, mg на R и mw 2 0 на 1/С(см. табл. 23.1). Тогда q в точке резонанса равна Lw /R, где w — ре­зонансная частота. В цепи с большой Q запасенная цепью энергия велика по сравнению с работой за один цикл, произ­водимой поддерживающей колебания в цепи машиной.

§ 2. Затухающие колебания

Вернемся к основной теме — переходным решениям. Пе­реходными решениями называются решения дифференциаль­ного уравнения, соответствующие ситуации, когда внешняя сила не действует, но система тем не менее не находится в покое. (Конечно, лучше всего решать задачу, когда сила не действует, а система покоится, покоится — ну и пусть покоится!) Соответ­ствующие переходным решениям колебания можно вызвать так: заставить силу поработать, а потом выключить ее. Что тогда случится с осциллятором? Сначала подумаем, как будет вести себя система с очень большой Q. Если сила действовала долго, то запасенная энергия была постоянной и работа тратилась лишь для того, чтобы поддержать ее. Предположим теперь, что мы выключили силу, тогда трению, которое раньше поглощало энергию поставщика, питаться больше нечем — кормильца-то нет. И трение начинает пожирать запасенную осциллятором энергию. Пусть добротность системы Q/2p=1000. Это значит, что работа, произведенная за цикл, равна 1/1000 запасенной энергии. Пожалуй, разумно предположить, что при не поддерживае­мых внешней силой колебаниях за каждый цикл будет теряться одна тысячная часть имеющейся к началу цикла энергии. Будем считать, что при больших Q изменение энергии описывается угаданным нами приближенным уравнением (мы еще вернемся к этому уравнению и сделаем его совсем верным!)

Уравнение это приближенное, потому что оно справедливо только для больших Q. За каждый радиан система теряет 1 /Q часть запасенной энергии Е. Значит, за промежуток времени dt энергия уменьшится в (wdt/Q раз (частота появляется при переводе радианов в настоящие секунды). А какая это частота? Предположим, что система устроена очень жестко, поэтому даже при действии силы она сколько-нибудь заметно колеблется толь­ко со своей собственной частотой. Поэтому будем считать, что w — это резонансная частота w 0. Таким образом, из уравнения (24.8) следует, что запасенная энергия меняется

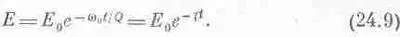
следующим образом:

Теперь нам известно значение энергии в любой момент. Какой будет приближенная формула, определяющая амплитуду коле­баний как функцию времени? Той же самой? Нет! Потенциаль­ная энергия пружины изменяется как квадрат смещения, кинетическая энергия — как квадрат скорости; это приводит к тому, что полная энергия пропорциональна квадрату сме­щения. Таким образом, смещение (амплитуда колебаний) будет уменьшаться с половинной скоростью. Иначе говоря, мы ожидаем, что решение в случае затухающего переходного дви­жения будет выглядеть как колебание с частотой, близкой к ре­зонансной частоте w 0; амплитуда этого колебания будет умень­шаться как ехр(-g t/2)

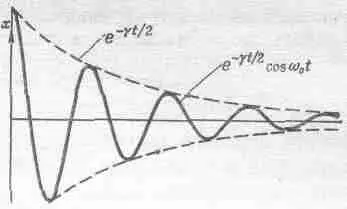
Эта формула и фиг. 24.1 дают представление о том, чего следует ожидать, а теперь приступим к точному анализу движе­ния, т. е. к решению дифференциального уравнения движения.

Фиг. 24.1. Затухающие колебания.

Как же решить уравнение (24.1), если выкинуть из него внешнюю силу? Будучи физиками, мы интересуемся не столько методом, сколько самим решением. Поскольку мы люди уже опытные, попытаемся представить решение в виде экспоненци­альной кривой, х=А exp(iat). (Почему мы так поступили? Оттого, что экспоненту легче всего дифференцировать!) Подставим это выражение в (24.1), помня о том, что каждое дифференцирование х по времени сводится к умножению на ia [напомним, что F(t)=0]. Сделать это очень легко, и наше уравнение примет вид