Ричард Фейнман - 2a. Пространство. Время. Движение

Если еще увеличить сопротивление, то колебания затухнут еще быстрее (фиг. 24.5).

Фиг, 24.5. Колебания почти исчезли.

Но если сопротив­ление увеличить сверх некоторого предела, колебаний мы вооб­ще не увидим. А может быть, нам просто отказывают глаза? Увеличим еще сопротивление и получим тогда кривую, пред­ставленную на фиг. 24.6; по ней можно лишь с натяжкой сказать, что в цепи произошли колебания, ну разве что одно.

Фиг. 24.6. Колебаний нет.

Можем ли мы математически объяснить это явление?

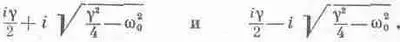
Сопротивление механического осциллятора, конечно, про­порционально g. В нашем случае g— это R/L. Теперь, если уве­личивать g, то в столь приятных нам решениях (24.14) и (24.15) наступает беспорядок; когда g /2 становится больше w 0, реше­ния приходится записывать по-другому:

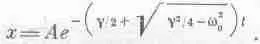
Это снова два решения, которые приводят нас к решениям exp(ia 1t) и ехр(ia 2t). Подставив теперь a 1, получим

Никаких колебаний. Чисто экспоненциальное убывание. То же самое дает и второе решение

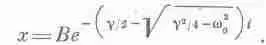
Заметим, что квадратный корень не может превысить g/2; даже если w 0=0, оба члена равны. Если же w 2 0отличается от g/ 2/4, то квадратный корень меньше g//2 и выражение в круглых скобках всегда положительно. Это очень хорошо! Почему? Да потому что если бы это выражение было отрицательным, то е пришлось бы возводить в положительную степень и мы по­лучили бы возрастающее со временем решение. Но при увели­чении в цепи сопротивления колебания не могут возрастать, зна­чит, мы избегли противоречия. Итак, мы получили два решения; оба решения экспоненциально затухают, но одно из них стре­мится «умереть» гораздо скорее. Общее решение, конечно, пред­ставляет собой комбинацию обоих решений, а значения коэф­фициентов А и В зависят от того, как начинаются колебания, каковы начальные условия. В нашей цепи случилось так, что А — отрицательное число, а В — положительное, поэтому на экране осциллоскопа мы увидели разность двух экспонент.

Давайте обсудим, как найти коэффициенты А и В (или А и A*), если известны начальные условия. Предположим, что в момент t=0 нам известны смещение х=х 0 и скорость dx/dt=v 0 . Если в соотношения

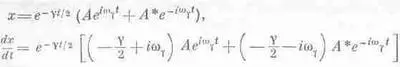
подставить значения t=0, х=х 0 , dx/dt=v 0 и воспользо­ваться тем, что е 0=е i 0=1, то мы получим

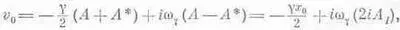
x 0 =A+A*=2A R ,

Значит,

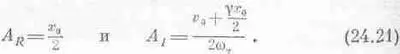
Таким образом, зная начальные условия, мы полностью определили А и А*, а значит, и кривую переходного решения. Можно записать решение и по-другому. Вспомним, что

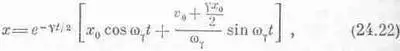
e i q+e - i q=2cosq и e i q - e - i q =2isin q , тогда

где wg=+Ц(w 2 0-(g 2/4). Мы получили формулу затухающих колебаний. Такая формула нам не понадобится, однако отметим ее особенности, справедливые и в более общих случаях.

Прежде всего поведение системы, на которую не действует внешняя сила, описывается суммой (суперпозицией) временных экспонент [мы записали их в виде exp(iat)]. Такое решение хорошо передает истинное положение вещей. В общем случае a — это комплексное число, и его мнимая часть соответствует затуханию колебаний. Наконец, тесная математическая связь синусоидальных и экспоненциальных функций, о которой го­ворилось в гл. 22, физически часто проявляется в переходе от колебаний к чисто экспоненциальному затуханию при крити­ческих значениях некоторых параметров системы (в нашем случае это было сопротивление g).

§ 1. Линейные дифференци­альные уравнения

§ 2. Суперпозиция решений

§ 3. Колебания в линейных системах

§ 4. Аналогии в физике

§ 5. Последовательные и параллельные сопротивления

§ 1. Линейные дифференциальные уравнения

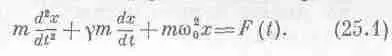
В этой главе мы снова вернемся к некоторым аспектам наших колебательных систем, только постараемся теперь увидеть нечто более общее, стоящее за спиной каждой частной системы. Изучение каждой колебательной системы своди­лось к решению дифференциального уравнения

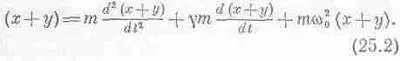
Эта комбинация «операций» над переменной х обладает интересным свойством: если вместо х подставить (х+у), получится сумма одинаковых операций над х и y, а умножение х на число а сводится к умножению на это число первона­чальной комбинации. Это легко доказать. Что­бы не переутомиться, записывая все буквы, вошедшие в (25.1), давайте введем «скоропис­ные» обозначения. Обозначим всю левую часть уравнения (25.1) символом L (х). Увидев такой символ, вы должны мысленно представить себе левую часть уравнения (25.1). Поэтому, соглас­но этой системе, символ L(x+y) будет озна­чать следующее:

(Подчеркнем букву L, чтобы не спутать этот символ с обычной функцией.) Иногда мы будем употреблять термин операторная запись, но со­вершенно безразлично, какими словами это называть, просто-напросто это «скоропись». Наше первое утверждение, что

L(x+y)=L(x)+L(y), (25.3)

следует из соотношений а(х+у)=ах+ау, d(x+y)/dt=dx/dt+-dy/dt и т. д.

Легко доказать, что для постоянного а

L(ax)=aL(x). (25.4)

[Соотношения (25.3) и (25.4) тесно связаны одно с другим, потому что, подставив в (25.3) х+х, мы получим (25.4) для част­ного значения а=2 и т. д.]

Решая более сложные задачи, можно получить L, в котором содержится больше членов и более высокие производные. Обыч­но первым делом интересуются, справедливы ли соотношения (25.3) и (25.4). Если они выполняются, то задачу называют линейной. В этой главе мы изучим некоторые свойства систем, следующие только из того факта, что система линейная. Это поможет нам понять общность некоторых свойств изученных ранее частных систем.