Ричард Фейнман - 2a. Пространство. Время. Движение

Чтобы придумать еще один пример принципа суперпозиции, спросите себя, как вам удается настроить свой радиоприемник на определенную радиостанцию, хотя одновременно работает очень много станций. Сигналы радиостанций — это колеблю­щиеся электрические поля очень высокой частоты, действую­щие на антенну радиоприемника. Амплитуда этих колебаний, правда, меняется, их модулирует голос диктора, но скорость этих изменений очень мала и об этом можно пока забыть. Когда вы слышите: «Станция работает на частоте 780 килогерц», это значит, что частота излучаемого антенной радиостанции элект­ромагнитного поля равна 780 000 колебаний в секунду и это поле с точно такой же частотой раскачивает электроны в ан­тенне вашего приемника. Но ведь в то же самое время поблизо­сти может работать и другая радиостанция на другой частоте, скажем на частоте 550 кгц. Эта станция тоже раскачивает электроны вашей антенны. Как же отделяются сигналы, посту­пающие в приемник с частотой 780 кгц, от сигналов, имею­щих частоту 550 кгц? Ведь вы же не слышали голоса обоих дикторов одновременно.

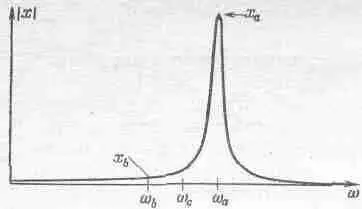
Первая часть электрической цепи радиоприемника — это линейная цепь. По принципу суперпозиции ее отклик на элект­рическое поле F а +F b равен х а +х b . По всему выходит, что нам придется слушать обоих дикторов сразу. Но вспомним, что в резонансной цепи кривая отклика х на единичную силу F за­висит от частоты примерно так, как это изображено на фиг. 25.3.

Фиг. 25.3. Резонансная кривая с острым максимумом.

В цепи с очень большим значением Q отклик имеет очень острый максимум. Предположим, что обе станции имеют примерно одинаковую мощность, поэтому обе силы имеют примерно оди­наковую амплитуду. Отклик равен сумме откликов х а и х b , но на фиг. 25.3 х а громаден, а х b очень мал. Таким образом, хотя оба сигнала одинаковы по силе, в приемнике они проходят через остро резонансную цепь, настроенную на частоту w а(частоту передач одной из станций), и отклик на эту частоту (станцию) значительно больше отклика на все остальные. Поэтому, не­смотря на то что на антенну действуют оба сигнала, полный отклик почти целиком составлен из частоты w а, и мы можем выб­рать ту станцию, какую пожелаем.

Несколько слов о механизме настройки. Как мы настраиваем радиоприемник? Мы изменяли частоту w 0, меняя L или С цепи, потому что частота цепи зависит от комбинации L и С. Боль­шинство радиоприемников устроено так, что в них меняется зна­чение С. Поворачивая ручку настройки приемника, мы изменяем собственную частоту цепи. Пусть какому-то положению ручки соответствует частота w с; если нет радиостанций, работающих на этой частоте, приемник молчит. Вы продолжаете изменять емкость С цепи, пока не построите кривую отклика с резонан­сом при частоте w b, тогда вы услышите другую станцию. Вот так и настраивается радиоприемник; все дело в принципе супер­позиции, в сочетании с резонансным откликом.

Чтоб закончить обсуждение, давайте подумаем, как посту­пить при анализе линейных задач с заданной силой, когда сила очень сложно зависит от времени. Можно поступать по-разному, но есть два особенно удобных общих метода решения таких за­дач. Первый метод: предположим, что мы можем решить зада­чу в некоторых частных случаях, например в случае синусои­дальных сил разных частот. Решать линейные уравнения в таких случаях — детская забава. Пусть нам и встретился этот «детский» случай. Теперь встает вопрос, нельзя ли представить любую силу в виде суммы двух или более «детских» сил? Мы уже показали на фиг. 25.1 довольно хитрую зависимость силы от времени; если туда добавить еще несколько синусоид, то ре­зультирующая кривая будет выглядеть еще сложнее. Таким образом, простенькие «детские» силы могут породить очень сложную силу. Верно и обратное: практически каждая кривая может быть представлена в виде бесконечной суммы синусоидаль­ных волн разной длины волн (или частоты). Таким образом, мы знаем, как представить заданную силу F в виде синусоидальных волн, поэтому решение х можно представить в виде суммы F синусоидальных волн, каждая из которых умножается на эф­фективное отношение х к F. Такой метод решения называют ме­тодом преобразования, Фурье, или анализом (разложением) Фурье. Мы не будем сейчас делать такого разложения; пока до­статочно только идеи.

Очень интересен другой способ решения сложных задач. Предположим, что кто-то после больших умственных усилий решил заданную нам задачу в случае одной частной силы — импульсной. Сила внезапно и быстро действует на систему, затем выключается и все опять спокойно. Нам теперь достаточно решить такую задачу лишь в случае единичной силы, потом умножением на подходящее число мы сможем получить любые силы. Мы знаем, что осциллятор откликается на импульсную силу затухающими колебаниями. А как быть в случае другой силы, например силы, изображенной на фиг. 25.4?

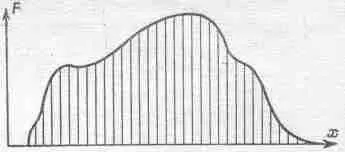
Фиг. 25.4. Сложную силу можно представить как последователь­ность коротких импульсов.

Такую силу можно представить в виде последовательных ударов молотком. Сначала всюду стоит тишина, потом кто-то берет в руки молоток и внезапно раздаются равномерные уда­ры — удар, удар, удар, удар, ... и опять все тихо. Иначе говоря, непрерывно действующую силу можно представить в виде ряда последовательных импульсов, быстро следующих один за дру­гим. Мы знаем последствия одного импульса, а последствием серии импульсов будет ряд затухающих колебаний; нарисуйте кривую колебаний для первого импульса, затем, немного от­ступя, такие же кривые для второго импульса, третьего и т. д. Потом сложите все кривые. Таким образом математически можно представить полное решение в случае произвольной силы, если можно решить задачу для импульса. Ответ для любой силы можно получить путем интегрирования. Это метод функции Грина. Функция Грина — это отклик системы на отдельный импульс, а метод функции Грина — это метод ана­лиза действия силы суммированием откликов на импульсы.

Физические принципы, лежащие в основе обоих методов, очень просты; они просто напрашиваются, если понять смысл линейного уравнения, но математические методы содержат до­вольно сложные интегрирования и т. д.; мы мало подготовлены, чтобы прямо атаковать эти методы. К этому вы еще вернетесь, когда поднабьете руку в математике. Но сама идея методов, право, очень проста.