Елена Чиркова - Как оценить бизнес по аналогии: Пособие по использованию сравнительных рыночных коэффициентов

Между финансовыми аналитиками существуют расхождения во взглядах, в каком размере нужно вычитать капиталовложения для расчета чистого денежного потока. Одни вычитают все инвестиции компании. Другие – только капиталовложения для поддержания существующего бизнеса, игнорируя при этом капиталовложения для роста. Объяснение простое: если уж речь зашла о капиталовложениях для роста, то для оценки такой компании лучше всего использовать модель дисконтированных денежных потоков, ибо очень трудно сравнивать компании с разными инвестиционными программами в растущий или новый бизнес на основе статичных мультипликаторов. Я с этим полностью согласна, вопрос только в том, всегда ли аналитику удается выделить из общих капиталовложений те, которые идут на поддержание существующего бизнеса, на основе публичной информации.

Мультипликатор «цена/дивиденды» (Price/Dividends – P/DIV [51] В русскоязычных текстах мне также встречался перевод «дивидендная доходность». Если читатель будет пользоваться данным термином, то его не следует путать с обратной формулой DIV1/P0, где P0 – цена акции в момент времени t = 0, а DIV1 – дивидендные выплаты в момент t = 1, т. е. имеется в виду, что инвестор соотносит полученные дивиденды с ценой акции на момент вложения в нее. В случае рассматриваемого нами мультипликатора имеется в виду цена акции на дату оценки. ) используется для так называемых дивидендных акций. Как правило, это акции крупных компаний со стабилизировавшимися операционными и финансовыми показателями [52] Таковой можно считать компанию, чьи темпы роста выручки и чистой прибыли примерно равны темпам роста национальной или мировой экономики (до 3–5 % в год). , регулярно выплачивающих дивиденды. Дивидендные акции по-английски называют еще стоимостными (value), в противоположность акциям быстрорастущих компаний (growth stocks).

Основная критика показателя P/DIV сводится к тому, что доходы инвестора в акции формируются не только за счет дивидендных выплат, но и благодаря росту их курсовой стоимости. Чем выше текущие дивиденды, тем меньше средств остается для финансирования инвестиционных проектов и тем медленнее будут расти прибыль и дивиденды в будущем, и наоборот. Иными словами, высокие дивиденды текущего года не обязательно должны означать более высокую оценку акций. В среднем на длительном временном интервале зрелая компания выплачивает в виде дивидендов определенный (более или менее фиксированный) процент чистой прибыли. Усредненные дивидендные выплаты можно взять за основу для расчета стоимости компании. Именно поэтому использование показателя P/DIV представляется наиболее корректным для компаний, у которых бизнес стабилен и дивидендные выплаты тоже стабилизировались. Я говорю о плюсах и минусах показателя P/DIV в первом разделе главы 11, см. подробности там.

Сейчас же посмотрим, как связаны между собой мультипликаторы Р/Е и Р/DIV. Вспомним, что согласно формуле (6)

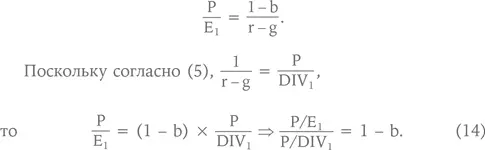
Таким образом, если каждый год 50 % чистой прибыли выплачивается в виде дивидендов, то P/E будет в два раза ниже, чем P/DIV. Формулу Гордона можно трансформировать и для случая, когда ожидается, что первые n лет компания будет находиться в фазе быстрого роста, при этом темпы роста прибыли составят g0 и будут выплачиваться относительно низкие дивиденды DIV0, так как прибыль будет направляться на финансирование роста. Затем темпы роста замедлятся до gn < g0, а дивиденды увеличатся до DIVn > DIV0. В этом случае формула Гордона примет следующий вид:

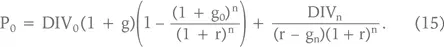
Необходимо отметить, что равенство (6) совершенно не дает нам основания полагать, что если дивиденды не выплачиваются (1 – b = 0 или b = 1), то акции ничего не стоят. Формулу можно переписать так, чтобы избавиться от разности 1 – b, обозначающей долю чистой прибыли, выплачиваемую в виде дивидендов. Таким образом, будет показано, что цена акций определяется доходностью компании, поэтому то, как чистая прибыль распределяется между дивидендами и нераспределенной прибылью (retained earnings), для цены акций не имеет значения. Дивиденды, не полученные сегодня, означают увеличение их размера завтра.

Посмотрим, что такое темпы роста g:

в свою очередь Et–1 = BVt–1 × ROEt–1, (17)

a Et = (BVt–1 + REt–1) × ROEt, (18)

где ROE (return on equity) – доходность акционерного капитала [53] Она измеряется отношением чистой прибыли компании E к чистой балансовой стоимости ее активов BV (book value of assets): ROE = E/BV. , a RE (retained earnings) – нераспределенная прибыль. Соответственно, из формул (16), (17) и (18) следует, что

при ROE = const,

g = ROE × b. (20)

Если теперь в формуле (14) мы заменим 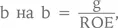что следует из (20), то получим, что

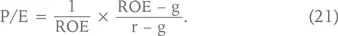
Таким образом, если доходность акционерного капитала компании равна доходности, требуемой инвесторами на свои вложения в эту компанию, т. е. Следовательно, P/E равен величине, обратной норме дисконта. Вот мы и объяснили наконец формулу, которая в начале книги вводилась на понятийном уровне. Как мы видим, в этом случае темпы роста прибыли g не влияют на величину P/E. Иными словами, для оценки стоимости неважно, выплачивается ли прибыль в виде дивидендов или вкладывается в инвестиционные проекты, если только инвестиции генерируют требуемую акционерами доходность r (вспомним теорему Миллера – Модильяни).

Если же ROE > r, то легко показать, что т. е. мультипликатор P/E у такой компании выше. Иначе говоря, в этом случае выгодно реинвестировать прибыль. Это понятно на интуитивном уровне, а также следует из математики: чем выше доля реинвестированной прибыли b, тем согласно (20) выше темпы роста прибыли g, а чем выше g, тем согласно (21) выше значение P/E при прочих равных. И наоборот, при ROE < r выгоднее выплатить дивиденды, так как в противном случае прибыль «разбазаривается» на низкодоходные проекты. Нужно отметить, что в долгосрочной перспективе для большинства компаний величина r приблизительно равна ROE, что обеспечивается колебанием курса акций: когда r < ROE, акции возрастают в цене, а при r > ROE – падают.