Александр Волошинов - Математика и искусство

"Закон сохранения искажений" еще раз убеждает нас в поразительной мудрости природы. Ведь если бы удалось найти систему перспективы, наиболее адекватную зрительному восприятию, то искусство живописи (по крайней мере, для художника-реалиста) должно было бы остановиться! Художнику не оставалось бы ничего, кроме как честно следовать этой наилучшей системе. И вот математика доказывает, что такой системы попросту нет, и последнее слово вновь остается за искусством!

Каковы же они, возможные научные системы перспективы? На рисунке показаны три варианта изображения условного пейзажа, взятые из книги Б. В. Paушенбаха "Системы перспективы в изобразительном искусстве. Общая теория перспективы". Горизонтальная поверхность Земли для большей наглядности разграфлена прямоугольной координатной сеткой. К цепи гор на горизонте ведет "дорога", проходящая по диагоналям прямоугольников. Вертикальные масштабы, построенные по правилам каждого варианта, показаны черными шестами, а прилегающие к ним белые шесты обозначают вертикальные размеры, соответствующие естественному зрительному восприятию. Все рисунки построены не "от руки", а рассчитаны согласно общей теории перспективы.

Вариант (а) соответствует системе перспективы, безошибочно передающей поверхность Земли (ширину и глубину пространства), а также дальний план (горы). Как видно из сравнения белых и черных шестов, неизбежные ошибки в этой системе смещены на вертикали, причем наибольшие ошибки допускаются при изображении вертикалей переднего плана, а по мере удаления к горизонту эти ошибки убывают. Здесь может воз никнуть естественный вопрос: а почему бы в этой системе, правильно передаю щей горизонтальные размеры, не пока зывать в соответствии с естественным восприятием и вертикальные линии? Тог да бы эта система стала "идеальной"? Однако такое насильственное вторжение в строение научной системы перспективы обернется тем, что при передаче полного пространства в изображении непрерыв них элементов появятся либо разрывы либо наложения одних элементов на другие. Подобные дефекты недопустимы, и поэтому в данном случае приходится жертвовать вертикалями.

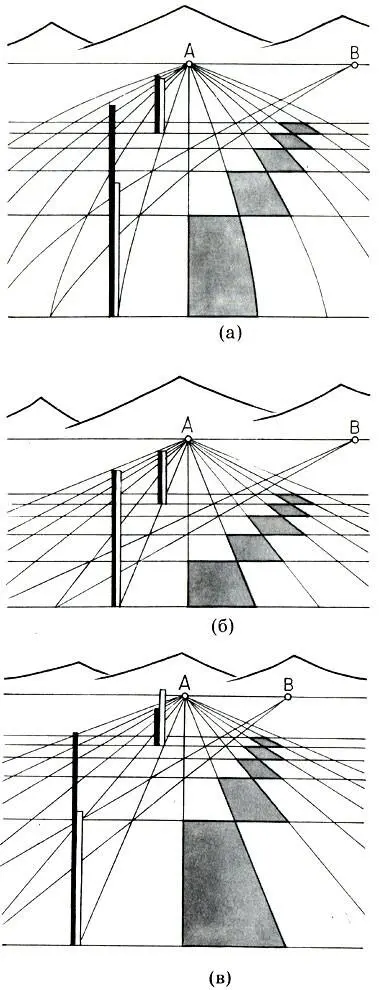
Возможные варианты научной перспективы: (а) — правильная передача поверхности земли; (б) — правильная передача вертикальных размеров; (в) — ренессансная перспектива. Рисунки Б. В. Раушенбаха

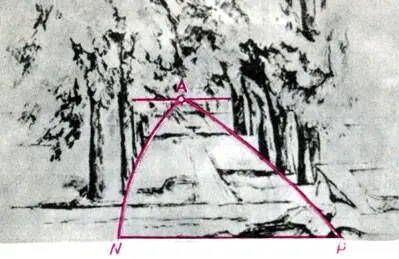
Сезанн. Каштановая аллея в Жа де Буффан. 1883-1887. Перспективный анализ Б. В. Раушенбаха

В варианте (б) ошибки в передаче вертикальных размеров исправлены. Более того, в этой системе правильно передается и ширина, а значит, сохраняется подобие фронтальных изображений. Однако какой "ценой" все это достигнуто, очевидно из самого рисунка: на нем крайне невыразительно, ослабленно передана глубина пространства, особенно глубина переднего плана.

Наконец, на рисунке (в) тот же условный пейзаж передан в ренессансной (линейной) системе перспективы. Сравнение этого рисунка с вариантами (а), (б) выявляет главный недостаток ренессансной системы: сильное преувеличение переднего плана и явное преуменьшение дальних объектов. Этот недостаток ренессансной (а значит, и фотографической) перспективы хорошо знаком альпинистам: запечатлев себя на фоне грандиозной горной панорамы, дома они обнаруживают на пленке жалкую гряду холмов на горизонте. Для среднего плана все ошибки ренессансной перспективы практически равны нулю.

Таким образом, анализ ошибок, неизбежно возникающих в той или иной системе перспективы, позволяет определить границы применимости известных систем перспективы и сделать выводы, которые были приведены на с. 317.

Анализ ошибок при изображении пейзажа (глубокого пространства) показывает, что в любой системе перспективы наибольшим искажениям подвержен именно передний план. Этот "закон наибольших искажений переднего плана" хорошо осознан художниками на практике. Поэтому при изображении пейзажа опытные мастера либо "отсекают" передний план границами картины, либо погружают его в тень.

Обратим внимание на то, что в варианте перспективы, правильно передающем глубину пространства (рис. а), образы прямых линий, уходящих к горизонту, становятся криволинейными (см. координатные линии, сходящиеся в точке А, и "дорогу"). Это свойство перспективы, правильно передающей глубину, было интуитивно "нащупано" некоторыми художниками XIX-XX вв., которые стали умело им пользоваться. А вот искусствоведы, подходившие к анализу живописи с позиций ренессансной системы перспективы либо приводившие в качестве аргументов фотографии (но это также линейная перспектива!), продолжали обвинять таких художников в своеволии и отступлении от "научных" канонов линейной перспективы.

Особенно "не повезло" здесь Полю Сезанну (1839-1906), чьи пейзажи в специальной монографии были тщательно сравнены с соответствующими фотографиями и где были указаны все его "ошибки". Возьмем, к примеру, акварель Сезанна "Каштановая аллея в Жа де Буффан". Эта акварель удобна для перспективного анализа тем, что ряды каштанов в натуре заведомо прямолинейны. Однако на акварели они явно искривлены, что и позволило сделать скоропалительный вывод о том, что Сезанн отступал от натуры. Однако, как показал Раушенбах, криволинейный треугольник ANP в соответствующем масштабе с удивительной точностью вписывается в криволинейную сетку координат на рисунке а (с. 325). Таким образом, именно горизонтальная поверхность Земли (а значит, и ряды каштанов) переданы Сезанном в полном соответствии со зрительным восприятием [39] Справедливости ради следует отметить, что Сезанн действительно иногда отступал от зрительных ощущений. Так, он часто преувеличивал размеры горы св. Виктории, которую ему хотелось видеть похожей, скорее, на гималайскую вершину. .

Не менее убедительным оказывается и сделанный Раушенбахом перспективный анализ этюда В. Д. Поленова (1844-1927) "Церковь св. Елены". Этот этюд был написан Поленовым в 1882 г. во время путешествия по Ближнему Востоку. В ренессансной системе перспективы (или на фотографии) образы параллельных линий равной высоты, проходящих по карнизам колонн и через середины (верхние точки) трех арок, должны быть прямолинейными. Как видно из иллюстрации, эти линии на этюде сильно искривлены. Пересекаясь на линии горизонта, они указывают на истинную главную точку картины, отмеченную кружком. Столь сильное искривление образов объективно прямых линий вызвано тем, что в изображаемом интерьере передний план вплотную приближен к зрителю. Однако такая геометрия этюда Поленова также не является "перспективной ошибкой", а, напротив, хорошо согласуется с вариантом (а), правильно передающим глубину пространства.