Александр Волошинов - Математика и искусство

На этом можно было бы поставить точку. Но мы поставили многоточие, ибо у вдумчивого читателя должен возникнуть еще один вопрос: почему все-таки октава разделена именно на 12 частей? Это вопрос из области математики, и ответ на него содержится в решении задачи, которую мы сформулируем так.

Требуется разделить интервал октавы 1≤f≤2 на n геометрически равных частей 1 = f 0≤f 1≤f 2≤...≤f n= 2, так, чтобы k-я точка деления приходилась на главный консонанс октавы — квинту, т. е. f k= 3/2 (0k= 2 k/n, то мы приходим к уравнению

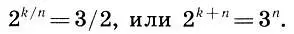(9.3)

Но левая часть уравнения (9.3) есть число четное при любых n и k, тогда как правая — число нечетное. Таким образом, мы пришли к противоречию, которое доказывает, что уравнение (9.3) в целых числах решений не имеет. Одновременно мы можем сделать важный вывод: шкала равномерно-темперированного строя никогда точно не пройдет через квинту.

Будем искать в целых числах приближенные решения уравнения (9.3). Логарифмируя, представим это уравнение в виде

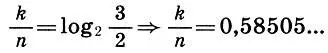(9.4)

и, как говорят математики, найдем рациональные приближения иррационального числа 0,58505... Такие задачи в математике решаются с помощью цепных дробей , т. е. дробей вида

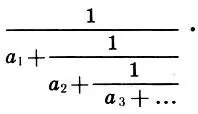(9.5)

Здесь a 1, а 2, а 3, ... — натуральные числа. Известно, что всякое число а∈[0; 1] можно разложить в цепную дробь (9.5), которая будет бесконечной, если число а иррациональное. Рациональные выражения

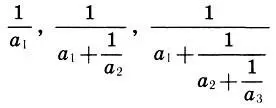
и т. д.

называются подходящими дробями цепной дроби (9.5), т. е. являются рациональными приближениями числа а.

Разложим число 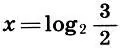в цепную дробь. По определению логарифма имеем

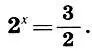(9.6)

Ясно, что х<1. Положим 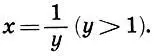Тогда (9.6) примет вид

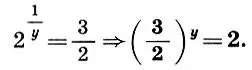(9.7)

Легко видеть, что 1

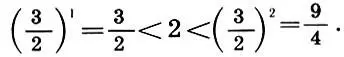
Поэтому положим

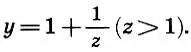
Уравнение (9.7) преобразуется к виду

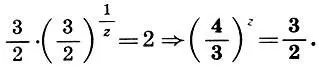(9.8)

Очевидно, что 1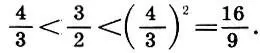Следовательно, полагаем

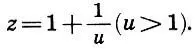
Тогда уравнение (9.8) примет вид

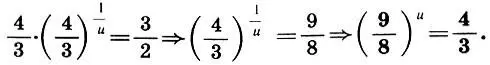(9.9)

Так как 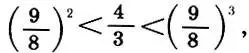, то для u получаем оценку 2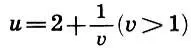и получаем

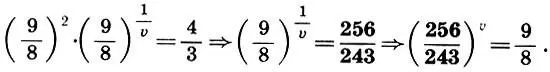(9.10)

С помощью таблиц логарифмов или простой проверкой на микрокалькуляторе находим оценку для v:2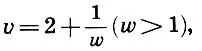отчего (9.10) примет вид

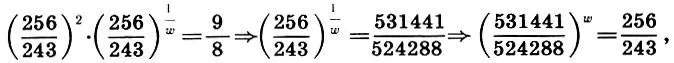
или

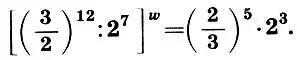(9.11)

Для w справедлива оценка 3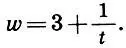

Не будем более испытывать терпение читателей (процесс разложения иррационального числа в цепную дробь все равно бесконечен). А в качестве компенсации за длинные выкладки обратим внимание на то, что в наших приближениях (9.6) — (9.11) все время фигурируют музыкальные интервалы: октава (2), квинта (3/2), кварта (4/3), тон (9/8), полутон (256/243) и даже пифагорова комма ((3/2)12:27)!

Построим теперь соответствующую цепную дробь:

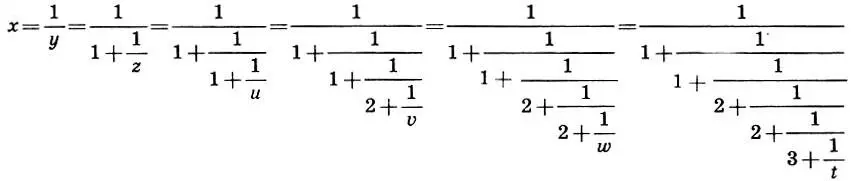
и выпишем подходящие дроби:

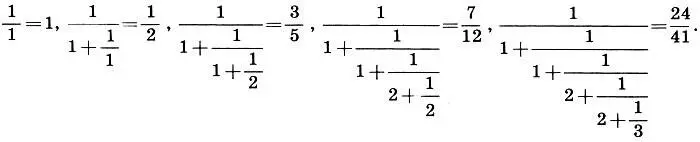
Первые три дроби 1; 0,5; 0,6 дают слишком грубое приближение к числу x = 0,58505... Четвертая дробь k/n = = 7/12 = 0,5833... является достаточно хорошим приближением. Она-то и положена в основу 12-звукового равномерно-темперированного строя (n = 12, k = 7, т. е. на седьмой ступени 12-звуковой гаммы находится темперированная квинта). Пятая дробь 24/41=0,58536 дает еще лучшее приближение. Таким образом, мы получаем еще одну равномерную темперацию, которая на 24-й ступени имеет практически идеальную квинту. Но ведь октава при этом делится на 41 ступень! Вряд ли кто отважится играть на столь сложном инструменте. Итак, именно 12-звуковая темперация является той "золотой серединой", которая обеспечивает достаточно чистое звучание консонансов при достаточной простоте музыкальной гаммы.

История создания равномерной темперации свидетельствует о том, как тесно порой переплетаются судьбы математики и музыки. Равномерная темперация в музыке появилась вслед за изобретением логарифмов и развитием алгебры иррациональных величин в математике. Без знания логарифмов провести расчеты равномерно-темперированного строя (8.8) было бы попросту невозможно. Логарифмы стали той "алгеброй гармонии", на которой выросла темперация.

И в заключение скажем несколько слов об одном любопытном и пока загадочном свойстве равномерной темперации. Согласно логике построения темперированной шкалы (9.1) все 12 мажорных , равно как и все 12 минорных, тональностей равномерно-темперированного строя должны звучать одинаково. Однако музыканты считают, что каждая тональность темперированного строя обладает своей неповторимой окраской. Так, композиторы единодушно сходятся в том, что до мажор характерен для светлого, солнечного настроения. Очень любил до мажор за жизнерадостность и оптимизм Бетховен. Вспомним 1-ю Симфонию и 1-й Концерт для фортепиано с оркестром Бетховена, написанные в до мажоре , которые как бы радостно перекликаются друг с другом; или его же 21-ю Сонату до мажор , названную за светлые и прозрачные тона именем богини утренней зари Авроры. Считается, что ми мажор выражает взволнованное, напряженное, мятущееся настроение. Поэтому именно ми мажор был так созвучен восторженной, страстно ищущей и терзаемой противоречиями душе Листа; в ми мажоре Листом написаны многие фортепианные произведения, транскрипции, "Фауст-симфония". В тональности фа диез мажор композиторы находят легкое, радостно возвышенное, романтическое настроение, столь характерное для творчества Шопена ("Баркарола", Экспромт соч. 36, Ноктюрн № 2 соч. 15). До минор считается тональностью мужественной печали, героико-трагических образов (вспомним огненный пафос "Патетической" сонаты Бетховена, знаменитый "революционный" этюд Шопена или шквальные кульминации 2-го Концерта для фортепиано с оркестром Рахманинова); ми бемоль минор - тональность глубоко трагических состояний. Например, Полонез № 2 соч. 26 — одно из самых скорбных творений Шопена.