Александр Волошинов - Математика и искусство

Мы не можем сказать, отражают ли такого рода суждения какие-либо неизвестные пока объективные закономерности, или это дань устоявшейся традиции. Если мы имеем дело с традицией, то ее корни следует искать в пифагоровом строе. Действительно, в пифагоровом строе энгармонические звуки не только нетождественны, но и принципиально отличаются друг от друга по своим качествам и выразительности. В пифагоровом строе соль диез , например, находится на пифагорову комму выше, чем ля бемоль. Поэтому соль диез тяготеет к верхнему звуку ля и воспринимается светлее, чем ля бемоль , который направлен к нижнему звуку соль и потому кажется более мрачным. Следовательно, и все повышенные звуки восходящей линии квинтового ряда (диезные звуки) имеют светлый характер, тогда как пониженные (бемольные) звуки нисходящей линии квинтового ряда (см. (8.2)) несут мрачный оттенок. Итак, все та же пифагорова комма окрашивает бемольные и диезные звуки в противоположные цвета — темные и светлые. Теперь становится понятным, почему Шопен написал свой знаменитый траурный марш из 2-й Сонаты соч. 35 в си бемоль миноре - тональности с пятью бемолями, а "Баркаролу" — самое утонченное и поэтическое из своих произведений, ставшее символом интимной лирики в музыке,- в фа диез мажоре - тональности с шестью диезами. Вот почему похоронный марш из 12-й Сонаты написан Бетховеном в ля бемоль миноре - тональности с наибольшим числом, семью бемолями, хотя, по мнению знатоков, эта находка Бетховена во многом теряет в равномерно-темперированном строе фортепиано.

Так что же такое есть индивидуальная окраска тональностей: традиция, идущая от пифагорова строя, или неизвестная объективная закономерность? Окончательного ответа на этот вопрос пока не существует.

Вот так, вместо обещанной точки в конце параграфа мы вновь пришли к вопросительному знаку. Но ведь это и хорошо, ибо новые вопросы зовут нас в новые пути в неизвестное! А впереди у нас, пожалуй, главный вопрос всей второй части: в чем секрет "закона Пифагора"? Почему приятные для "уха" консонансные интервалы математически выражаются такими приятными для "разума" простыми целочисленными соотношениями 2/1, 3/2, 4/3, 5/4, 6/5?

Ноябрьским утром 1717 г. на ступенях парижской церкви святого Жана ле Рона был найден младенец. Его взяли на воспитание и в честь святого церкви окрестили Жаном ле Роном. Мальчик рано проявил блестящий ум и жадную любознательность и вскоре стал гордостью всей Франции. Это был Жан ле Рон Д'Аламбер (1717-1783) — выдающийся французский математик, философ, писатель, член Парижской, Петербургской и других академий.

Круг интересов Д'Аламбера был необычайно широк: механика (принцип Д'Аламбера), гидродинамика (парадокс Д'Аламбера), математика (признак сходи мости Д'Аламбера), математическая физика (формула Д'Аламбера), философия теория музыки. Такой широты требовала и oабота вместе с Дени Дидро над созданием наменитой "Энциклопедии наук, искусств и ремесел", да и сам дух эпохи посвещения, когда к знаниям тянулись все, в том числе и "просвещенные деспоты" Фридрих II и Екатерина II. Последуя неоднократно приглашала Д'Аламбера быть воспитателем ее сына — цесаревича Павла, назначая при этом баснословное вознаграждение, но всегда получала деликатный, но твердый отказ.

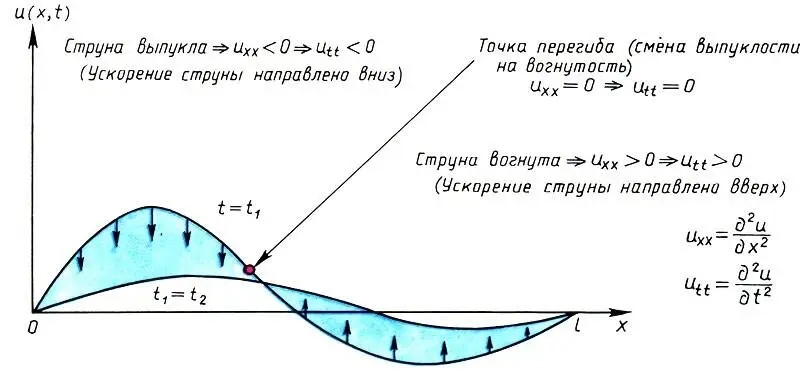
Колебания струны длины l. Показаны два момента времени t 12. Масштаб по ординате U(х,t) сильно увеличен

В 1747 г. Д'Аламбер опубликовал статью "Исследования по вопросам о кривой, которую образует натянутая струнa, приведенная в колебание", где впервые задача о колебании струны сводилась к решению дифференциального уравнения в частных производных. И хотя эта тема выходит за рамки школьной математики но ведь в знаниях "держать себя в рамках" — значит погубить свою любознательность!), мы рассмотрим простое и поистине красивое уравнение, описывающее колебание струны, так называемое полновое уравнение, с которого началась новая ветвь математики — математическая физика:

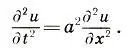(10.1)

Здесь t — время; х — координата струны в положении равновесия; u = u(х, t) — неизвестная функция, выражающая отклонение точки с координатой х в момент времени t от положения равновесия; а 2— коэффициент пропорциональности, характеризующий упругие свойства струны 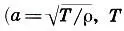, T — сила натяжения струны, р — плотность однородной струны). Предполагается, что струна совершает малые колебания, происходящие в одной плоскости. Наконец, символы 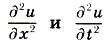обозначают частную производную второго порядка, которая определяется как производная от производной 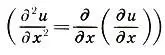. Частные производные — 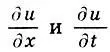, как и обычная "школьная" производная 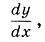характеризует скорость изменения функции u(х,t) по каждой из переменных х или t в отдельности при условии, что другая переменная не изменяется (у функций одной переменной y = y(x) — одна производная, а у функции двух переменных u = u(х,t) — две частные производные 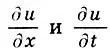. Чтобы отличать частные производные от обыкновенных "школьных", пишут не прямую букву 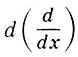, а круглую .

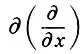Волновое уравнение (10.1) есть не что иное, как следствие второго закона Ньютона. Левая часть (10.1) выражает вертикальное ускорение струны в точке х, а правая часть — отнесенную к массе струны силу, вызывающую это ускорение, которая тем больше, чем больше вогнутость струны .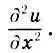

Д'Аламбер нашел общее решение уравнения (10.1)

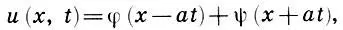(10.2)

которое содержит две произвольные функции φ(х,t) и ψ(х,t). Через пять лет Даниил Бернулли (1700-1782), математик, механик, физиолог и медик, почетный член Петербургской Академии наук, представитель славного рода Бернулли, который к настоящему времени подарил миру более 100 потомков, добившихся значительных результатов во всех сферах человеческой деятельности, и прежде всего в научной, получил другое общее решение уравнения (10.1)