Джо Боулер - Математическое мышление

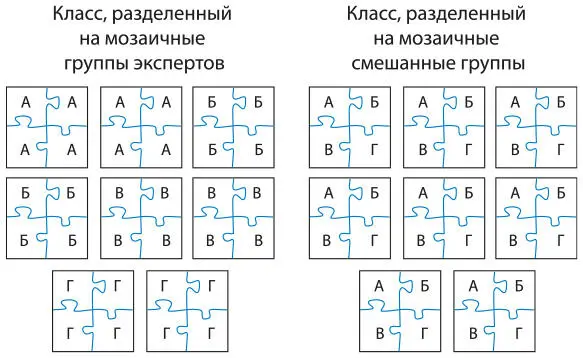
Рис. 8.3.Мозаичные группы

В главе 6я предложила мозаичное занятие, в ходе которого ученики стали экспертами по вдохновляющим примерам, призванным искоренить стереотипы о том, кто может добиться больших успехов в математике.

Еще одно мозаичное занятие стимулирует учеников к осмыслению существующих в алгебре связей между графиками, таблицами значений, членами уравнения и закономерностями. Учитель раздает ученикам листы с четырьмя закономерностями, такие как в примерах 8.5–8.8, и предлагает группам учеников сделать плакат, иллюстрирующий, как они представляют себе рост фигур, и показывающий таблицу значений, график уравнения, а также закономерность, обобщенную и смоделированную с помощью уравнения. Каждый член группы становится экспертом по нескольким формам представления закономерности. Затем учитель вызывает по одному участнику из каждой группы. Все делятся знаниями о своей задаче с другими членами группы.

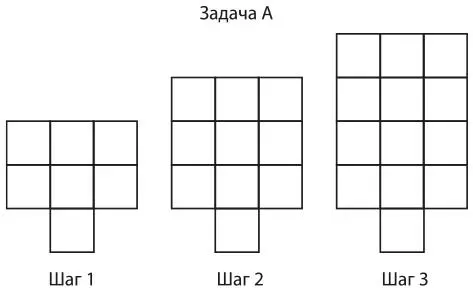
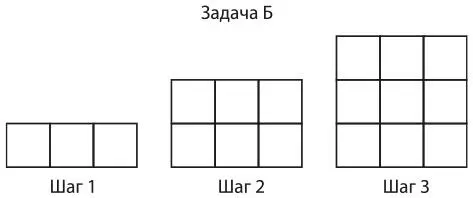
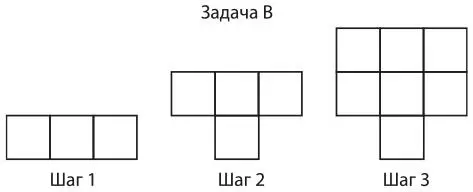
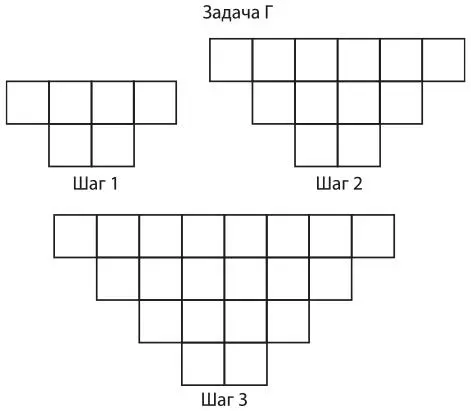
Затем группы обсуждают сходства и различия между разными формами представления своих алгебраических закономерностей.

Когда ученики становятся экспертами и несут ответственность за обучение других, это стимулирует их взять на себя ответственность за новые знания, которые они получают.

6. Билет на выход

Билет на выход — лист бумаги, который вы выдаете ученикам в конце урока и в котором предлагаете рассказать о своем обучении (пример 8.9). Прежде чем уйти из класса, ученики заполняют эти листы и сдают их. Они могут поразмышлять, что способствует их обучению и дает учителям ценную информацию об обучении и идеи для следующего урока.

Билет на выход _____ Имя _____ Дата _____

Талон на выход _____ Имя _____ Дата _____

7. Онлайн-формы

Я видела, как учителя используют эффективную стратегию, состоящую в том, чтобы предложить ученикам заполнить онлайн-форму в режиме реального времени за время урока и отправить ее на адрес учителя. Можно попросить учеников поделиться комментариями или мыслями по поводу урока. Ученики, которые обычно не принимают активного участия в устном обсуждении, более охотно поделятся своими мыслями в онлайн-режиме. Существует много разных способов использования этой стратегии; в частности, можно попросить учеников прислать свои размышления, предложить проголосовать по какому-то вопросу или показать учителю красный, желтый или зеленый индикатор, который не увидят другие ученики.

8. Рисование в свободной форме

Как было отмечено в главе 4, наука о головном мозге говорит нам, что процесс обучения протекает наиболее эффективно, когда мы используем разные пути в мозге. Этот вывод имеет огромные последствия, которые выходят далеко за рамки методов оценки.

Изучение математики, особенно формальной и абстрактной, на которую приходится б о льшая часть школьной программы, становится эффективнее, когда ученики используют визуальное и интуитивное математическое мышление в сочетании с числовым. Поистине эффективный способ стимулировать учеников к этому сводится к тому, чтобы предложить им нарисовать свои идеи (рис. 8.4).

Рис. 8.4.Математический рисунок в свободной форме

Вместо того чтобы предлагать ученикам записать, что они понимают, во время размышлений на уроке или после урока, попросите их изобразить свое понимание в виде эскиза или комикса. Если вы хотите увидеть и даже показать своим ученикам очень интересные и забавные рисунки о математических концепциях, рекомендую некоторые видео Вай Харт, которые можно найти по следующим адресам.

Спирали, последовательность Фибоначчи — представьте себе, что вы растение (часть 1): https://www.youtube.com/watch?v=ahXIMUkSXX0&list=PLF7CBA45AEBAD18B8&index=8.

Вечеринка треугольников: https://www.youtube.com/watch?v=o6KlpIWhbcw&list=PLF7CBA45AEBAD18B8&index=7.

9. Ученики сами пишут вопросы и тесты

Предложите ученикам написать свои вопросы или критерии оценки для других. Само формулирование правильного вопроса поможет сфокусироваться на том, что важно, и позволит мыслить творчески, что уже важно. Ученики получают истинное удовольствие, когда им дают задание написать утверждения для оценки работы по математике.

Комментарии

Все представленные выше стратегии позволяют достичь целей первых двух частей трехэтапного процесса оценки для обучения: эти стратегии помогают ученикам понять, что они изучают и что должны изучить.

Части 1 и 2 процесса оценки для обучения играют очень важную роль сами по себе, а часть 3 дает ученикам поддержку, которую не может предоставить никакой другой метод. Это крайне важная часть процесса оценки для обучения, позволяющая ученикам понять, как преодолеть разрыв между тем, где они есть, и тем, где должны быть. В этой области есть один метод, который превосходит остальные по своей эффективности: процесс, в ходе которого учителя дают ученикам комментарии по поводу их работы. Величайший дар, который вы можете передать своим ученикам, — ваши знания, идеи и обратная связь об их математическом развитии, наряду с позитивными высказываниями и сигналами по поводу мышления роста.

Эллен Круз — одна из тех учителей, с которыми я работала в школьном округе Виста. Во время наших занятий по профессиональному развитию я поделилась с Эллен и другими учителями результатами исследований, о которых шла речь выше, продемонстрировав им положительное влияние комментариев в качестве альтернативы оценкам. Эллен — удивительная и преданная делу учительница, которая работает в непростой школе, находящейся на этапе «улучшения программы». Ведь штат Калифорния отнес эту школу к числу работающих недостаточно эффективно. В ней разнородный состав учеников: 90% — латиноамериканцы, а оставшиеся 10% приходятся на другие этнические группы. 43% учеников изучают английский язык и 86% имеют право на бесплатные обеды. Эллен рассказала мне, что, когда она начала преподавать в этой школе, руководство было сфокусировано на тестировании, что типично для школ, получивших ярлык «улучшенная программа». Вопросы тестов и тесты по учебным разделам в точности воспроизводили вопросы стандартного с несколькими вариантами ответов. Школа была сосредоточена на «улучшении» (звучит неплохо), и учителя часами сидели над отчетами, сгенерированными программами для проведения тестов, отслеживая закономерности. Затем каждому ученику присваивали определенный цвет, а учителям говорили, что «синие» успешно справятся с тестом штата, а у «красных» почти нет шансов. Учителям говорили, что они должны сосредоточиться на нижнем сегменте «зеленых» учеников и на верхнем сегменте «желтых», поскольку повышение их успеваемости окажет самое большое влияние на результаты тестирования.