Джо Боулер - Математическое мышление

Попытки «улучшения» заслуживают похвалы, но метод, который применила эта школа (что типично для школ, проходящих процедуру улучшения программы), выдвигал на первый план группы учеников, способных повысить результаты тестирования, а не делал упор на потребностях конкретных учеников. Школа сначала распределила детей по результатам тестов, а затем и по цветам, от которых зависело, кто получит меньше внимания (ими оказались ученики как с высокой, так и с низкой успеваемостью). Такой подход, подразумевавший работу с детьми как со статистическими показателями, которыми можно манипулировать, используется везде в США, как правило, в ответ на жесткие суждения и ярлыки, навешиваемые во имя «улучшения».

В разгар внедрения культуры достижений, навязанной этой школе, Эллен решила провести среди учеников опрос. Как и следовало ожидать, она обнаружила высокий уровень тревоги в связи с тестами. Ученики сдавали многочисленные тесты, а учителям дали указание постоянно подчеркивать важность эффективной работы в условиях стресса. Эллен хотела изменить эту культуру и для начала отменила тесты по разделам и заменила их оценкой более мелких учебных модулей. Эллен прекратила использовать слова «тест» и «проверка» и назвала свои мини-экзамены возможностью «показать, что вы знаете». Вопросы с несколькими вариантами были исключены, ученикам предлагали ответить на математические вопросы. Кроме того, Эллен прекратила готовить учеников к эталонным экзаменам на уровне школьного округа; она проводила такие экзамены без предупреждения, чтобы предотвратить усиление тревоги, советуя ученикам: «Сделайте всё возможное и ни о чем не беспокойтесь». Результаты тестов не ухудшились, несмотря на отсутствие предварительной подготовки и сосредоточения на тестах, а уровень тревожности учеников снизился. Важно то, что, как сказала мне Эллен, дети начали получать удовольствие от уроков математики.

Но Эллен (как и другие думающие, неравнодушные учителя) не остановилась на этом, а предприняла следующие шаги для улучшения ситуации. В следующем году Эллен и ее коллеги — преподаватели математики в восьмом классе, Аннет Уилсон и Анджела Тайнсенд, — перестали ставить ученикам оценки, а использовали листы с математическими утверждениями. Кроме того, все учителя этой группы изменили названия своих систем оценки на такое: «Покажите, что вы можете сделать» (пример 8.10).

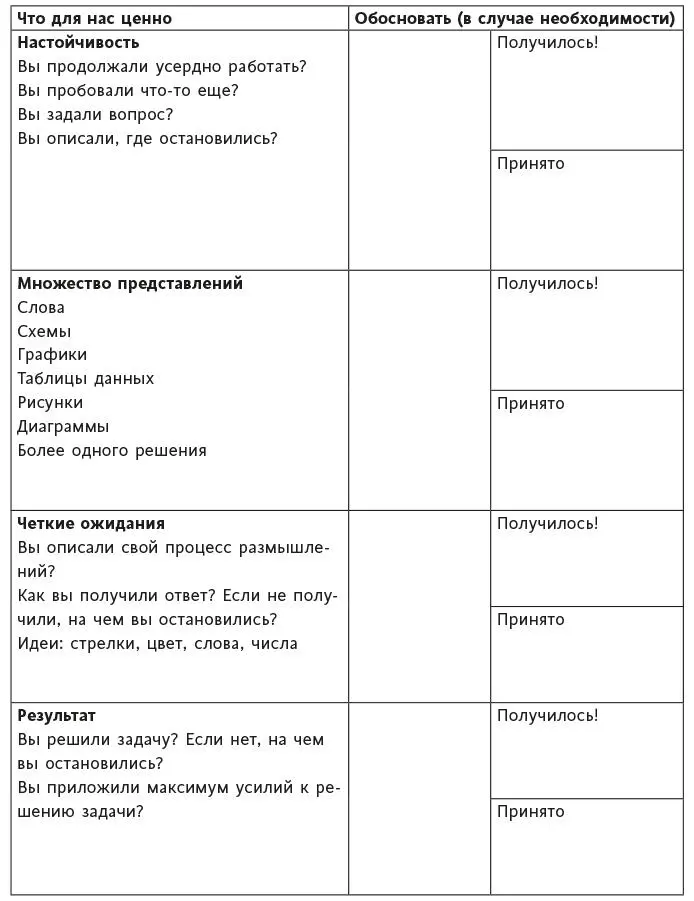
Источник: предоставлено Эллен Круз.

Когда эта группа учителей прекратила ставить оценки, используя вместо них комментарии, ученики начали читать и интерпретировать эту обратную связь и время от времени задавать вопросы. Эллен ставила оценки только тогда, когда ученики просили ее об этом. Она сказала мне, что поначалу ей приходилось тратить слишком много времени на обратную связь, которую она регулярно предоставляла всем своим 110 ученикам, и она научилась писать комментарии тогда, когда это приносило максимальную пользу ученикам. Это идеальный подход к обратной связи. Он отнимает не больше времени, чем проверка заданий или выставление оценок, но приносит гораздо больше пользы ученикам. Периодическая обратная связь, предоставляемая в профессионально рассчитанные важные моменты, — бесценный дар, но его не следует применять слишком часто.

Эллен рассказала мне, что сейчас гораздо больше учеников старательно занимаются математикой и она видит, как они стремятся работать с полной отдачей. Идеальный результат. Эллен рассказала также об усовершенствованиях в ее методах преподавания, проистекающих из полезной информации, которая получена благодаря новым формам оценки и которую она использует для планирования обучения. За годы, прошедшие после того, как Эллен внесла изменения в свой подход к преподаванию и оценке, отметки учеников, которые переходят в старшие классы, существенно улучшились, а количество неудач с изучением алгебры в старшей школе сократилось вдвое.

К сожалению, многие учителя вынуждены ставить оценки, поскольку того требует школьный округ или руководство школы. Теоретически они должны ставить оценки только в конце курса, а не во время его прохождения, когда школьникам нужна информация о том, как учиться лучше, которую необходимо предоставлять в рамках формативного оценивания. Ниже представлен список рекомендаций, как справедливо ставить оценки и при этом подавать ученикам позитивные сигналы о мышлении роста.

1. Всегда давайте ученикам возможность повторно представить любую работу или сдать тест, чтобы получить более высокую оценку.Это сильнейший сигнал о мышлении роста, который говорит ученикам, что вас заботит обучение , а не одни только результаты. Некоторые учителя говорят мне, что это несправедливо: ученики могут самостоятельно изучить то, что им необходимо, чтобы улучшить свою оценку. Но мы должны ценить такие усилия, ведь они направлены на обучение.

2. Сообщайте об оценках руководству школы, а не ученикам.Если в вашей школе надо ставить оценки до завершения курса, не обязательно сообщать о них ученикам. Предоставьте им вербальную или диагностическую обратную связь о способах улучшения результатов.

3. Используйте многоплановую систему выставления оценок.Учителя могут считать математику обширной дисциплиной и ценить многоплановый подход к ее изучению на уроках, но при этом оценивать работу учеников только по тому, дают ли они правильные ответы на процедурные вопросы. Лучшие учителя, с которыми я работала и которые ставили оценки, рассматривали скорее работу учеников, а не результаты тестов — записывая, например, задают ли они вопросы, представляют задачи разными способами, рассуждают и обосновывают свой выбор и опираются на размышления друг друга. Иными словами, такие учителя оценивают многоплановость математики. В случае оценки разных способов выполнения работы гораздо больше учеников успешно справляются с заданиями.

4. Не применяйте 100-балльную шкалу.Один из самых несправедливых и бессмысленных с математической точки зрения методов выставления оценок — когда учителя используют несколько заданий в качестве основы для оценки, исходя из того, что каждое из них оценивается в 100 баллов, и присваивая 0 баллов за любое незаконченное, отсутствующее или неправильно выполненное задание. Дуглас Ривз (Reeves, 2006) доказал, что такая практика противоречит логике: разрыв между оценками A, B, C и D составляет 10%, а между D и F — 60%. Следовательно, отсутствие какого-либо задания может означать, что ученик получит вместо оценки A оценку D. Ривз рекомендует использовать четырехбалльную шкалу (A = 4, B = 3, C = 2, D = 1, F = 0), в которой все интервалы равны, вместо шкалы, которая не имеет смысла с математической точки зрения: