Джо Боулер - Математическое мышление

В период прохождения определенного курса очень важна формативная, а не суммативная оценка знаний учеников. Кроме того, подход оценки для обучения, который можно также считать оценкой для мышления роста, предлагает ряд стратегий и методов.

Один из важных принципов оценки для обучения состоит в том, что такой подход возлагает на учеников ответственность за их обучение. По сути, оценка для обучения сводится к предоставлению учащимся возможности стать самостоятельными, самим регулировать учебный процесс и определять, что им необходимо изучить в первую очередь, а также знать, как улучшить свои показатели. Оценку для обучения можно рассматривать как процесс, состоящий из трех частей: предоставление детям четкой информации о том, что они изучили; помощь ученикам в осознании того, где они сейчас и где должны быть; информирование учеников о способах преодоления разрыва между тем, где они есть и где должны быть (рис. 8.1).

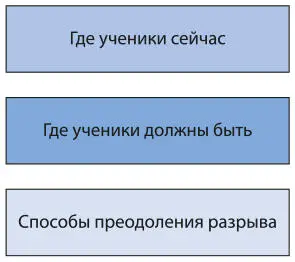
Рис. 8.1.Оценка для обучения

Этот подход обозначается термином оценка для обучения , а не оценка обучения : информация, которую получают учителя и ученики благодаря ему, позволяет учителям сделать свое преподавание более эффективным и помогает ученикам работать с полной отдачей. Учителя, которые используют оценку для обучения, тратят меньше времени на то, чтобы рассказывать ученикам об их успеваемости, и уделяют больше времени созданию возможностей для того, чтобы дети взяли обучение под свой контроль. Учитель из Англии, который начал использовать этот метод, сказал, что это заставило его меньше сосредоточиваться на себе и больше на детях (Black et al., 2002). Он укрепил уверенность в себе как в учителе благодаря эффективным стратегиям создания возможностей для того, чтобы ученики сами продвигали вперед свое обучение.

Самые сильные ученики — те, которые склонны к размышлениям, занимаются метапознанием (размышляют о том, что знают) и берут обучение под свой контроль (White & Frederiksen, 1998). У традиционных уроков математики есть один серьезный недостаток: ученики редко знают, что они изучают и где находятся в более широком контексте. Они сосредоточены на методах, которые им необходимо запомнить, но зачастую даже не знают, над какой областью работают. Я неоднократно присутствовала на уроках математики и часто останавливалась возле парт учеников, чтобы спросить их, над чем они работают. Часто ученики просто называют задание. Многие из моих диалогов с ними выглядели примерно так.

Дж. Б.:Над чем вы работаете?

Ученик:Над упражнением 2.

Дж. Б.:Так что же вы делаете на самом деле? Какой материал изучаете?

Ученик:Ой, извините, это вопрос 4.

Научное исследование, которое провели Барбара Уайт и Джон Фредериксен (White & Frederiksen, 1998), убедительно продемонстрировало важность размышлений. Эти исследователи изучили учеников 12 седьмых классов, изучающих физику. Они разделили учеников на экспериментальные и контрольные группы. Все изучали тему «Сила и движение». Ученики контрольных групп уделяли часть каждого урока обсуждению этой работы, а ученики экспериментальных групп на уроках занимались самооценкой и взаимным оцениванием в соответствии с критериями той дисциплины, которую изучали. Результаты исследования оказались весьма неожиданными. Ученики, у которых раньше была низкая успеваемость, добились самых больших успехов. Уделив какое-то время анализу профильных критериев и оценке своей работы в соответствии с ними, они начали добиваться таких же результатов, что и ученики с высоким уровнем успеваемости. Ученики средних классов получили даже более высокие результаты тестирования по курсу физики старшей школы, чем ученики, которые прошли углубленный курс физики. Исследователи пришли к выводу, что низкая успеваемость объясняется скорее не отсутствием у учеников соответствующих способностей, а тем, что раньше они просто не знали, на что им обращать внимание.

К сожалению, это касается многих. Крайне важно довести до сведения учеников, что именно им следует изучать. С одной стороны, это помогает им понять, что такое успех, а с другой — запускает процесс самоанализа, который оказывается бесценным инструментом обучения.

1. Самооценка

Самооценка и взаимная оценка — две основные стратегии, позволяющие ученикам повысить свою осведомленность о том, какую тему они изучают, а также о более широких путях ее исследования. В случае самооценки ученикам дают четкие утверждения по теме, которые они используют для размышлений о том, что они уже изучили и над чем им еще нужно поработать. Такие утверждения должны иметь математическое содержание, например: «Я понимаю разницу между средним и медианным значением и когда каждое из них следует использовать», а также описывать методы работы, например: «Я научился проявлять настойчивость в решении задач и продолжаю работать, даже если задачи трудные». Если ученики начинают каждый раздел работы с четких утверждений об изучаемой теме, они фокусируются на более широком контексте: узнают, что важно, над чем нужно поработать, чтобы улучшить свои знания. Исследования свидетельствуют: когда ученикам предлагают оценить свой уровень понимания, они не завышают и не занижают его (Black et al., 2002).

Самооценку можно проводить на разных уровнях детализации. Учителя могут использовать в листах самооценки критерии, охватывающие урок или более длительный период, например учебный модуль, четверть и полугодие. Ниже приведены примеры критериев самооценки за более короткий и более длинный промежутки. Помимо них, ученикам необходимо предоставить время для размышлений о своем обучении, что они могут сделать во время урока, в конце урока или даже дома.

Лист самооценки из примера 8.1 предоставлен Лори Мэллет, замечательной учительницей третьего класса, с которой я работала. Лори принимала участие в летнем семинаре по профессиональному развитию, который я проводила и на котором мы рассматривали все способы стимулирования мышления роста. Она предлагает ученикам три варианта выбора.

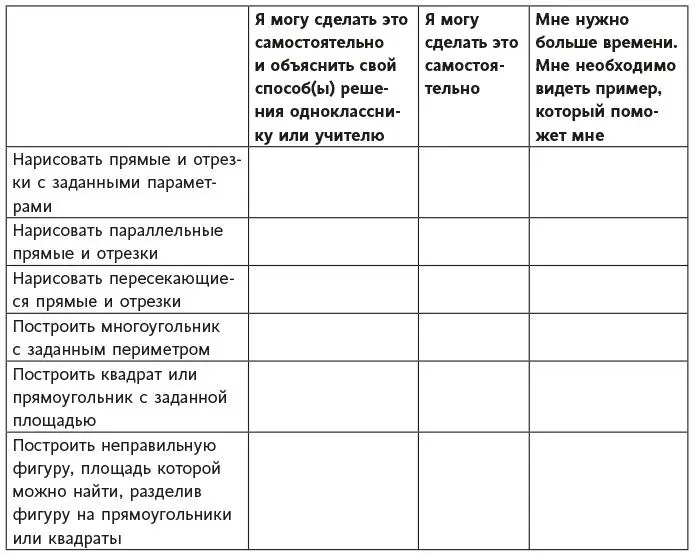
Вместо утверждений, над которыми должны размышлять ученики, некоторые учителя (особенно те, которые учат детей младшего возраста) используют смайлики вроде тех, которые показаны на рис. 8.2.

Рис. 8.2.Смайлики для самоанализа