Джо Боулер - Математическое мышление

В ходе видеоисследования TIMSS был проведен сравнительный анализ подхода к преподаванию в США и других странах. По результатам был сделан вывод о том, что в США уроки «в милю шириной и дюйм глубиной» (Schmidt et al., 2002), а в других странах, особенно в Японии, они носят более концептуальный и глубокий характер, подразумевают более активное обсуждение изучаемого материала учениками. Этот анализ позволил установить связь между глубиной обсуждения и работы в Японии (в отличие от США) и более высоким уровнем успеваемости в стране (Schmidt et al., 2002; Schmidt, McKnight, & Raizen, 1997).

Многие родители не понимают важность математической глубины; они ошибочно полагают, что их детям пойдет на пользу ускоренное изучение материала. Такие родители делают все возможное, чтобы их дети досрочно переходили в следующие классы и им как можно раньше преподавали математику на углубленном уровне. Но изучение математики — не гонка, а математическая глубина вдохновляет учеников и обеспечивает их вовлеченность и эффективную работу, готовя их к углубленному изучению математики в будущем. Именно ученики, которых вынуждают быстрее проходить материал, чаще всего при первой же возможности бросают математику (Jacob, 2015; also Boaler, 2015b). Необходимо, чтобы все ученики занимались математикой с полной отдачей; ни для кого она не должна быть слишком легкой и никого нельзя заставлять повторно отрабатывать те или иные концепции, если он уже усвоил их. Один из лучших и самых важных способов стимулирования сильных учеников состоит в том, чтобы дать им возможность глубже изучать концепции. Причем они могут делать это вместе с другими учениками, которые способны глубже проанализировать эти концепции в другие дни. В работе со своими студентами из Стэнфорда я использую такой метод: предложить тем, кто закончил задание, расширить его, двигаясь в новом направлении.

Недавно я поставила своим студентам из Стэнфорда задачу под названием «Раскрашенный куб» и раздала им коробки с кубиками сахара, чтобы они могли смоделировать ее (пример 9.7 и рис. 9.7).

Представьте себе куб 5 × 5 × 5, внешние грани которого раскрашены в один цвет, причем этот куб состоит из меньших кубиков размером 1 × 1 × 1.

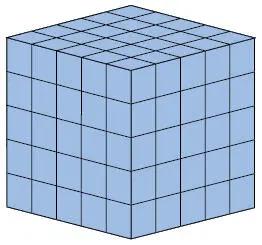
Ответьте на следующие вопросы.

У скольких маленьких кубиков будет 3 раскрашенные грани?

У скольких маленьких кубиков будет 2 раскрашенные грани?

У скольких маленьких кубиков будет 1 раскрашенная грань?

У скольких маленьких кубиков не будет раскрашенных граней?

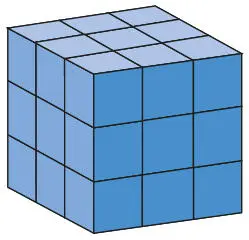
Рис. 9.7.Раскрашенный куб 3 × 3 × 3

Некоторые студенты выполнили задачу, построив куб меньшей размерности (например, 3 × 3 × 3) из кубиков сахара, и разрисовали внешние грани, чтобы проанализировать распределение кубиков с разным количеством раскрашенных граней. Я сказала им, что после решения задачи для куба размерами 5 × 5 × 5 они могут расширить задачу каким угодно способом. Это была лучшая часть урока: у студентов появлялось гораздо больше возможностей для обучения, поскольку разные группы анализировали, например, как найти решение задачи с пирамидой вместо куба (рис. 9.8); одна группа анализировала соотношения в пирамиде, составленной из пирамид меньшего размера, а еще одна работала над соотношениями в случае перемещения куба в четвертое измерение, а затем и в n -е.

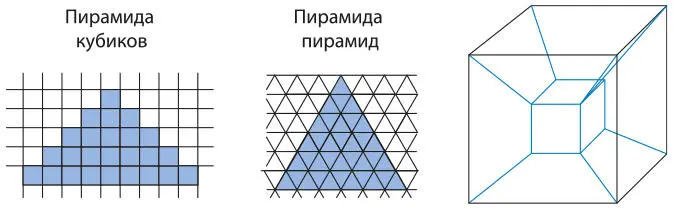
Рис. 9.8.Расширенная задача с кубом

Если дать ученикам возможность расширять задачи, они почти всегда находят творческие и увлекательные возможности для углубленного анализа математических концепций, что для них очень ценно.

Свяжите математику с реальным миром с помощью моделирования

Школьники объясняют свою неприязнь к математике в первую очередь ее абстрактным характером и якобы несоответствием реальному миру. Как ни печально, это отражает преподавание математики в школе: ведь на самом деле она повсюду. Она настолько важна для успешной жизни, что ее назвали новым «гражданским правом» — важным элементом эффективного функционирования в обществе (Moses & Cobb, 2001). Когда я проводила интервью с группой молодых людей в возрасте 24 лет, которые только что получили традиционное математическое образование, и спросила их о роли математики в их жизни и работе, они выразили разочарование в связи с полученным образованием. Эти молодые люди сказали, что видят математику повсюду в окружающем мире и каждый день используют ее в своей работе, но опыт ее изучения в учебных заведениях не дал им ощущения реальной природы математики и ее важности для их будущего. По их словам, если бы они знали, что математика — не мертвая дисциплина, не имеющая отношения к реальности, и что она может сыграть важную роль в их взрослой жизни, это полностью изменило бы их мотивацию на уроках в школе.

Необходимость сделать математику интересной и связанной с реальным миром часто приводит к тому, что ее ставят в ситуацию, которую я называю «псевдоконтекстом» (Boaler, 2015a), призванным отражать реальность. Ученики работают над придуманными задачами из реального мира, которые далеки от реальности, как в случае поездов, которые мчатся навстречу друг другу по одному пути. Такой контекст не помогает ученикам узнать, что математика — полезная дисциплина. Он создает противоположное впечатление: будто математика — нечто чуждое и нереальное. Чтобы ученики могли успешно решать искусственные задачи из реального мира, им предлагают представить себе, что ситуация реальна, игнорируя при этом все, что они знают о жизни. Возьмем в качестве примера такие типичные задачки.

• Джо может выполнить работу за 6 часов, а Чарли — за 5 часов. Какую часть работы они могут выполнить, работая вместе 2 часа?

• Ресторан берет 2,5 доллара за 1/ 8часть пирога. Сколько стоит весь пирог?

• Пицца разделена на 5 кусочков для 5 друзей на вечеринке. Три друга съедают свои кусочки пиццы, но потом приходит еще 4 друга. На сколько частей следует поделить два оставшихся кусочка пиццы? (Boaler, 2015a)

Все эти вопросы взяты из опубликованных учебников, подобные задачи дети решают на уроках математики. Однако они лишены смысла. Всем известно, что люди работают вместе не с той же скоростью, что и по отдельности; рестораны назначают другую цену на большие порции, а если на вечеринку приходит больше друзей, заказывают еще одну пиццу — никто не режет оставшиеся кусочки. В итоге дети приходят к выводу, будто математика не имеет отношения к реальной жизни. На самом деле многие считают, что, приходя на урок математики, они попадают в Страну математики — причудливое и загадочное место, которое требует, чтобы они оставили свой здравый смысл за дверью.