Джо Боулер - Математическое мышление

Откройте ученикам мир закономерностей; дайте им активную роль в отслеживании закономерностей во всех областях и на всех уровнях.

В главе 3я говорила о Мариам Мирзахани, математике и моей коллеге из Стэнфордского университета. Она попала в сводки новостей во всем мире, когда стала первой женщиной, получившей Филдсовскую премию. Обсуждая огромный вклад Мариам в развитие математики, специалисты говорили о связи ее работы со многими областями этой науки, такими как дифференциальная геометрия, комплексный анализ и динамические системы. Мариам размышляла так: «Мне нравится пересекать воображаемые границы, которые люди устанавливают между разными областями. Это очень воодушевляет… Есть так много инструментов, и ты не знаешь, какой из них сработает. Все дело в том, чтобы быть оптимистом и пытаться находить связи между разными вещами». Мне хотелось бы, чтобы все ученики мыслили так же.

Когда ученики устанавливают и видят связи между разными методами, они начинают понимать истинную математику и получают от нее гораздо большее удовольствие. Это особенно важно для вовлечения большего числа девочек в различные области STEM (подробнее см. главу 6). Стандартная учебная программа часто препятствует установлению связей, поскольку представляет математику как набор разрозненных тем. Но учителя могут и должны восстанавливать связи, постоянно рассказывая о них, подчеркивая их важность и предлагая ученикам поразмышлять о связях и обсудить их. На видео, представленном на сайте YouCubed, показано, как тема пропорционального рассуждения связывает дроби, графики, треугольники, коэффициенты, теорему Пифагора, таблицы, фигуры, угол наклона и умножение (YouCubed at Stanford University, 2015c; http://www.youcubed.org/tour-of-mathematical-connections). Мы сняли это видео, чтобы продемонстрировать связи между разными областями математики (о существовании которых ученики, возможно, даже не подозревали), и помочь им размышлять о таких связях. На основании этого видео учеников необходимо стимулировать к исследованию и поиску математических связей разными способами.

Ниже представлено несколько способов привлечения внимания к связям в математике.

• Поощряйте учеников предлагать разные методы решения задач, а затем найти связи между ними, например обсудив их сходства и различия и почему можно использовать один метод, а не другой. Это можно сделать с методами, которые используются для решения числовых задач (см. рис. 5.1 в главе 5).

• Предложите ученикам находить связи между математическими концепциями в процессе работы над задачами. Например, обратите внимание на две математические задачи, представленные в примере 9.4 и на рис. 9.4.

Сколько существует способов разделить 24 собачьи галеты на две группы?

Сколько существует способов разделить 24 собачьи галеты на равные группы?

Представьте полученный результат в графическом виде, отображающем все комбинации.

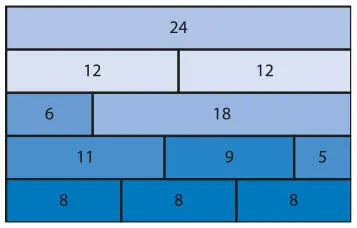
Рис. 9.4.Решение задачи с собачьими галетами

Учителя могут предложить ученикам представить решение более чем в одной форме и связать числа в своих решениях с диаграммами, что позволит задействовать разные пути в головном мозге. Некоторые ученики могут использовать бумагу в клетку, другие — числовую ось, еще кто-то — воспользоваться кубиками или другими мелкими предметами. Учителя могут предложить ученикам поразмышлять о разных методах, которые можно использовать для деления на равные группы (в частности, сложение и умножение), а также о том, как эти методы связаны друг с другом.

В разных заданиях, представленных в примере 9.5, ученики должны сфокусироваться на разных областях математики и связях между ними. Успешные ученики — не те, которые представляют себе математику как набор разрозненных тем (такой точки зрения придерживается большинство учеников). Успешными можно считать скорее тех, кто воспринимает ее как совокупность взаимосвязанных концепций (Program for International Student Assessment (PISA), 2012). Именно такой подход учителя должны активно поощрять, особенно если учебники создают противоположное впечатление. Математика как совокупность связей вдохновляет и притягивает учеников, и все учителя могут создать условия для того, чтобы дети увидели связный характер математики.

Представьте дроби 3/ 4, 6/ 8и 12/ 16в виде графиков.

Представьте эти дроби в виде подобных треугольников.

Чем схожи и отличаются эти формы представления дробей — в виде чисел, графика и треугольников? Можете ли вы применить цветовое кодирование к различным свойствам каждой формы представления, чтобы эти свойства были представлены одним цветом в разных представлениях?

Обучайте учеников творческому и визуальному подходу к математике

На своих уроках я стимулирую творческий подход, ставя интересные задачи и придавая большое значение мыслительному процессу. Я говорю, что меня не интересует быстрота выполнения; мне нужно интересное представление идей, творческий метод или решение. Когда я использую такой подход к постановке математических задач, ученики всегда удивляют меня своим творческим мышлением.

Очень важно добиться того, чтобы ученики применяли визуальное мышление в процессе решения задач по математике. Это обеспечивает доступ к пониманию и задействованию разных путей в головном мозге. Аманда Кунлаба — учительница четвертого класса, которая объединяет искусство с основными школьными предметами, в том числе математикой. Она рассказывает, как однажды спросила своих учеников, элементы каких уроков искусства им больше всего понравились в основных школьных предметах. Она вспоминает, как один ученик «спокойно, но с воодушевлением объяснил, что ему нравится изобразительное искусство, поскольку творчество помогает ему “забыть о плохом”, и что ему это необходимо “чаще одного раза в неделю”» (Koonlaba, 2015).

Искусство и визуальное представление играют не только терапевтическую и творческую роль, хотя это очень важно. Они играют также решающую роль в обеспечении доступа к пониманию разных предметов. Когда я предлагаю детям визуализировать идеи и представить их в графическом виде, это всегда приводит к повышению уровня вовлеченности и созданию новых возможностей понимания математических концепций. Некоторым ученикам визуальное представление дается с трудом, но именно им использование этого подхода приносит самую большую пользу.

Кроме того, учителя должны постоянно предлагать ученикам связывать идеи, представленные в визуальной форме, с числовыми или алгебраическими методами и решениями. Как показано в главе 5, цветовое кодирование — хороший способ стимулировать установление таких связей. В следующих двух примерах мы видим, насколько цветовое кодирование может улучшить понимание учениками таких концепций, как геометрические фигуры, дроби и деление. В предыдущих главах приведены примеры применения цветового кодирования для алгебраических выражений и параллельных прямых. Когда ученики осваивают соотношения углов, им можно предложить раскрасить разные углы треугольника, разрезать рисунок и выстроить углы в линию, чтобы увидеть соотношения между ними. Визуальное представление углов поможет запомнить эти соотношения.