Валентин Арьков - Применение гистограмм в управлении качеством

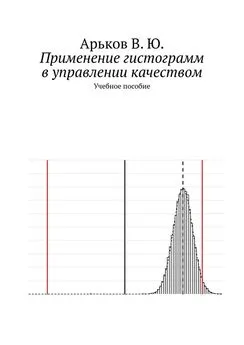
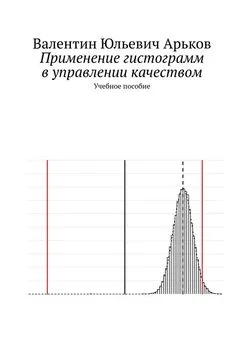
Рис. 9.1.3. Оценка среднего

Рис. 9.1.4. Хвосты распределения

Для нулевого варианта задания имеем:

Среднее = ВГД — 2 сигмы = 1040 — 2 x 5 = 1030.

Далее мы будем моделировать случайную величину с этими параметрами:

Задание. Оцените среднее и сделайте зарисовку формы распределения на поле допуска.

Проведём анализ гистограммы, как описано в предыдущих разделах:

— С помощью надстройки моделируем случайную величину со средним 1030 мм и сигмой 5 мм. Задаём новое начальное состояние генератора случайных чисел (рис. 9.1.5).

— Вычисляем выборочное среднее.

— Проводим группировку данным.

— Строим гистограмму.

— Строим кривую нормального распределения с параметрами выборки.

— Наносим границы допуска и номинал, а также выборочное среднее.

— Изучаем и описываем гистограмму.

Рис. 9.1.5. Генератор

Для всех линий на графике строим вспомогательные таблички (рис. 9.1.6).

Рис. 9.1.6. Вспомогательные таблички

Задание. Постройте вспомогательные таблички.

Строим график, наносим все линии и делаем необходимые настройки. Получаем окончательное оформление гистограммы (рис. 9.1.7).

Рис. 9.1.7. Оформление гистограммы

На графике видно, какая часть гистограммы выходит за верхнюю границу допуска, — как мы и планировали. Можно увидеть отклонение среднего от номинала. Форма гистограммы соответствует нормальному распределению.

Задание. Постройте и оформите гистограмму.

Сигма (среднее квадратичное отклонение) — вторая по важности характеристика распределения. Этот параметр определяет разброс вокруг среднего значения. Если ухудшаются свойства или настройки оборудования, может увеличиваться технологический разброс. Тогда хвосты распределения могут выйти за границы допуска — даже при поддержании среднего в районе номинала.

Смоделируем следующую ситуацию (рис. 9.2.1):

Среднее = Номинал

НГД = Среднее — 2 Сигмы

ВГД = Среднее +2 Сигмы

Рис. 9.2.1. Увеличенная сигма

В нулевом варианте получаем:

Сигма = 20 мм.

Задание. Определите сигму и сделайте зарисовку распределения на поле допуска с указание размеров.

Скопируем предыдущую страницу электронной таблицы и вставим её в конец рабочей книги:

Move or Copy — Create a Copy — (move to end).

Это наш шаблон для вычислений и построения графика.

Окончательный вид гистограммы приводится на рис. 9.2.2.

Рис. 9.2.2. Оформление гистограммы

Задание. Сгенерируйте данные и постройте гистограмму.

Нарушение симметрии распределения может происходить по разным причинам. Например, возможны ситуации, когда есть физический предел для минимального значения, а максимальное значение не ограничено. Такими показателями могут быть количество жалоб, аварий или отказов. Их минимальное количество равно нулю, а отрицательные значения невозможны. При этом распределение будет скошено влево. Естественно, при анализе гистограммы необходимо учитывать физическую природу производственного процесса и понимать, есть ли предпосылки к асимметрии. Если нарушение симметрии не обусловлено естественными причинами, потребуется провести исследование — особенно если за некоторое время до этого распределение было близко к нормальному.

Вопрос. Когда возникает асимметрия распределения?

Для моделирования асимметричного распределения используем бета-распределение со следующими параметрами:

Alpha = 2

Beta = 5.

Это стандартное асимметричное распределение, хорошо изученное в теории вероятностей. Его используют, в частности, для оценки длительности работ при управлении проектами. Название указывает на то, что в расчётах используется специальная математическая Бета-функция. Сейчас мы не углубляемся в математические дебри. В данной работе нас будет интересовать только форма графика и возможности имитационного моделирования.

Познакомимся с формой бета-распределения. Используем следующую функцию:

BETA. DIST (x, alpha, beta, cumulative).

Создаём столбец значений от 0 до 1 с шагом 0,01.

Находим значения функции плотности вероятности (probability density function, PDF):

BETA. DIST (x, 2, 5, 0).

Строим график функции (рис. 9.3.1). График начинается в точке х = 0. Можно видеть явное нарушение симметрии.

Рис. 9.3.1. Бета-распределение

Задание. Постройте график бета-распределения.

В теории вероятностей уже определили теоретическое среднее для такого распределения. Формула среднего для бета-распределения приводится на рис. 9.3.2.

Рис. 9.3.2. Среднее для бета-распределения

Задание. Вычислите значение среднего с точностью до пяти знаков после запятой.

Сформируем график желаемого распределения (рис. 9.3.3). Нам нужно преобразовать случайную величину со стандартным бета-распределением в то, что показано на зарисовке. Нам придётся сделать пересчёт координат в порядковые номера — чтобы нанести кривую распределения на комбинированную диаграмму..

Рис. 9.3.3. Зарисовка распределения

Задание. Сделайте зарисовку для пересчёта координат.

Разберёмся, как нам предстоит проводит пересчёт координат. Для номинального размера 1000 ммслучайная величина b(аргумент бета-распределения) должна быть равна среднему значению, то есть 0,29. Для размера 1020 ммаргумент равен 1. Строим пропорцию и получаем значение «икса» при b = 0 (рис. 9.3.4).

Рис. 9.3.4. Оценка параметров распределения

Нам нужно расположить случайную величину в поле допуска, как показано на зарисовке рис. 9.3.3. Для этого мы сгенерируем случайную величину b, а затем преобразуем её следующим образом:

x = 992 +28 b.

Как мы получили эту формулу? Мы определили, что начало кривой b = 0 будет в точке х = 992. Это смещение по оси «икс». В формуле пересчёта это свободный член уравнения.

Случайная величина bменяется от 0 до 1. При этом размер детали, то есть величина х, меняется от 992 до 1020. Это в 28 раз больше. Получаем масштабный коэффициент 28.

Задание. Составьте формулу для преобразования случайной величины.

Переходим к имитационному моделированию. Будем использовать метод ФУНКЦИОНАЛЬНОГО ПРЕОБРАЗОВАНИЯ. Чтобы сгенерировать случайные числа с заданным распределением, вначале генерируют равномерное распределение, а потом к нему применяют обратную функцию заданного распределения (рис. 9.3.5). Здесь F (x) — интегральная функция заданного распределения, p (x) — функция плотности вероятности. Пока что выглядит довольно сложно. Как это работает — мы постепенно разберём.