Хаим Шапира - Восемь этюдов о бесконечности. Математическое приключение

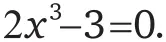
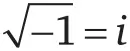
– алгебраическое число (но не вещественное число), так как является решением уравнения x ² + 1 = 0.

Золотое сечение ϕ – алгебраическое число, так как является решением уравнения x ² − x − 1 = 0.

Короче говоря, алгебраические числа «многочисленны», потому что «многочисленны» уравнения с многочленами вида

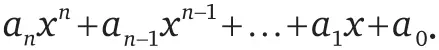
С учетом этого следующее утверждение может показаться несколько удивительным:

Множество алгебраических чисел счетно.

Доказательство.Рассмотрим уравнение

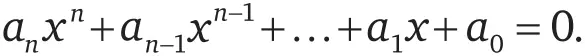
Предположим, что a n – положительное число. Если это не так, мы можем умножить все уравнение на (–1); получившееся уравнение будет иметь те же корни.

Подобно тому, как мы разбирались с расселением рациональных чисел в гостинице, определим для каждого многочлена «высоту» Н .

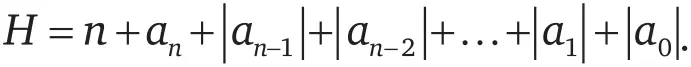
Символ | m | обозначает абсолютное значение (или модуль) числа. Если число положительно, его абсолютное значение равно ему самому: | 37 | = 37. Если число отрицательно, абсолютное значение становится положительным: |–234 | = 234.

Теперь мы можем выписать все уравнения (некоторые из которых не имеют решений) в порядке возрастания высоты.

Например, для Н = 1 существует всего один многочлен, и он представляет собой просто 1, то есть не зависит от х, и дает уравнение 1 = 0, не имеющее решений. Это уравнение не имеет смысла и не дает нам никаких алгебраических чисел.

Для Н = 2 мы получаем два уравнения: х = 0 и 2 = 0. Первое дает алгебраическое число 0, а второе снова оказывается бессмысленным и не имеет корней.

Для Н = 3 получаются следующие уравнения: 3 = 0, х – 1 = 0, 2 х = 0, х + 1 = 0, и наконец, х ² = 0. Первое из этих уравнений не дает алгебраических чисел, а из остальных мы получаем два новых алгебраических числа: 1 и –1.

Я надеюсь, что основная идея понятна.

Дойдя до Н = 5, мы встретимся с √2 (убедитесь в этом самостоятельно). Для каждого значения высоты существует конечное количество уравнений, и каждое уравнение имеет конечное число решений; следовательно, при каждом значении высоты мы добавляем конечное количество алгебраических чисел. Это доказывает, что множество алгебраических чисел – это на самом деле набор, состоящий из счетного числа конечных множеств. Следовательно, алгебраические числа легко можно разместить в бесконечной гостинице Гильберта. Это означает также, что множество алгебраических чисел счетно и его мощность – ℵ 0.

В это довольно трудно поверить, но мощность множества чисел, делящихся на пухплекс в степени пухплекса, равна мощности множества алгебраических чисел.

Доказать, что множество счетно, совсем не трудно. Нужно всего лишь найти одно-однозначное и сюръективное соответствие с множеством натуральных чисел. Проблема сводится к следующему: чтобы доказать, что то или иное множество счетно, достаточно показать, что его элементы могут быть расположены в некотором последовательном порядке, но, чтобы доказать , что множество несчетно, необходимо доказать, что не существует абсолютно никакого способа расположить его элементы последовательно. Это похоже на «задачу» доказательства, что в комнате есть по меньшей мере один муравей, в сравнении с задачей доказательства, что нигде в комнате ни одного муравья точно нет. Как только мы найдем хотя бы одного муравья, мы получим доказательство первого утверждения, но то, что мы не находим муравьев в данный момент, совершенно не означает, что какой-нибудь муравей не найдется позже.

Как я уже отмечал, в 1891 г. Георг Кантор предложил замысловатый метод, помогающий доказать невозможность подсчета количества разнообразных объектов, – он называется «диагональным методом Кантора». Мы уже встречались с этим методом, когда профессор Финкельштейн-Островский-Канторович доказывал, что в бесконечной гостинице невозможно разместить числа, заключенные между 0 и 1, десятичное представление которых содержит только цифры 0 и 1. При помощи того же самого метода можно доказать, что и множество всех чисел, заключенных между 0 и 1, несчетно (докажите это!). В этом нет ничего неожиданного, поскольку множество «чисел, заключенных между 0 и 1, десятичное представление которых содержит только цифры 0 и 1» – это собственное подмножество множества всех чисел, заключенных между 0 и 1. Кроме того, если вспомнить, что любое существующее число может быть записано в двоичной системе счисления с использованием только цифр 0 и 1, можно легко убедиться, что мощность этих двух множеств должна быть одинаковой (почему?).

Бесконечные множества чисел, которые невозможно расположить в последовательном порядке, называются – что и неудивительно – несчетными. Множество всех точек на числовой прямой, заключенных между 0 и 1, несчетно, и его мощность не равна ℵ 0. Следовательно, для обозначения мощности множества всех вещественных чисел (или любого отрезка прямой вещественных чисел) нужен новый символ! В качестве такого символа используют букву ℵ [50] В русской математической литературе чаще используется малая готическая . – Примеч. ред . Говорят, что ℵ – мощность континуума. Однако следует отметить, что несчетные множества не всегда имеют мощность ℵ.

Поскольку концепция канторовой диагонали не только красива, но и важна, я объясню ее еще раз – теперь на примере доказательства, что множество всех слов бесконечной длины, составленных с использованием только двух букв (a и b), невозможно подсчитать. Другими словами, такое множество несчетно.

Если вы уже поняли объяснение, которое профессор Финкельштейн-Островский-Канторович дал Омеге относительно чисел в десятичной системе счисления, у вас не должно вызвать затруднений и следующее изложение. Речь идет в точности о том же самом, только на другом примере. Если вы не вполне поняли первое объяснение, я надеюсь, что вы поймете его на этот раз.

Доказательство будет строиться от противного, то есть мы предположим, что справедлива противоположная гипотеза: все такие слова можно расположить в некой последовательности. Затем мы увидим, что это предположение приводит к противоречию, что означает, что наша исходная гипотеза была ложной.