Хаим Шапира - Восемь этюдов о бесконечности. Математическое приключение

А вот утверждение, которое может показаться еще более странным. Можно (сходным образом) доказать, что мощность любого отрезка прямой равна мощности бесконечного луча. Приведенный ниже чертеж иллюстрирует эту идею в самом общем виде. Если вы внимательно посмотрите на нее, то, я уверен, сообразите, как построить соответствие между конечным отрезком и бесконечным лучом.

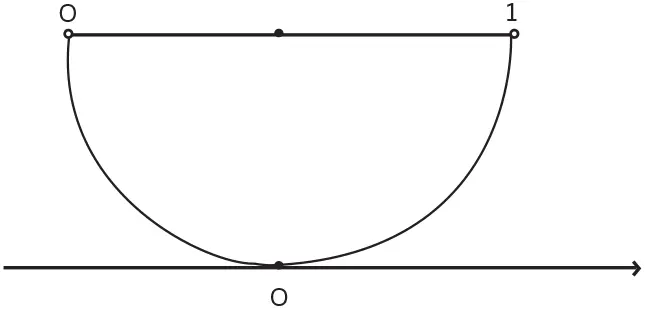
Это означает, что и отрезок прямой длиной один миллиметр, и отрезок прямой длиной миллиард километров, и даже бесконечный отрезок прямой содержат равное «количество» точек. Этот результат может показаться менее удивительным, если вспомнить, что у точки на самом деле нет ни длины, ни площади, ни объема. Зенон спросил бы, как эти «бездлинные» точки могут образовывать прямую длиной 107 «чего-нибудь» или даже бесконечный луч.

Если отойти от простых прямых, лучей и отрезков, Кантор доказал также, что существует одно-однозначное и сюръективное соответствие между точками отрезка прямой и точками квадрата или куба!

Что еще удивительнее и невероятнее, Кантор доказал существование одно-однозначного и сюръективного соответствия между бесконечной прямой и n -мерным пространством (для любого n !).

Открою вам секрет: это открытие оказалось чрезмерно радикальным даже для самого Кантора. Вот как он отозвался о нем: «Je le vois, mais je ne le crois pas!» – «Вижу, но не верю!»

Возможно, вы помните, что, дав выше определение алгебраических чисел, я отметил, что числа, не относящиеся к алгебраическим, называются трансцендентными. Исходя из нашего открытия, что мощность множества вещественных чисел выше мощности множества чисел алгебраических, по-видимому, можно предсказать, что трансцендентные числа существуют, то есть что имеются числа, не являющиеся корнями выражений типа

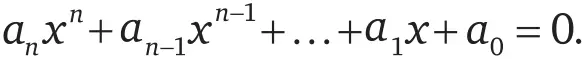
Но где они? Хотя концепция трансцендентных чисел существует уже давно, вплоть до XIX в. никто не мог с уверенностью сказать, что «видел» такое число.

Доказательство существования таких чисел дал не Георг Кантор. Оно было получено в 1844 г. выдающимся французским математиком Жозефом Лиувиллем. Однако Кантор развил результаты Лиувилля, показав, что трансцендентные числа составляют большинство всех чисел. Другими словами, числа в большинстве своем не только не рациональны; по большей части числа даже не относятся к алгебраическим.

Множество трансцендентных чисел несчетно.

Доказательство.Множество всех вещественных чисел можно разбить на два непересекающихся множества – множество алгебраических чисел и множество трансцендентных чисел. Слово «непересекающиеся» означает, что ни один элемент не может принадлежать обоим множествам.

Обозначим множество алгебраических чисел буквой А, трансцендентных – буквой Т, а вещественных – буквой R.

Объединение двух множеств А и В, обозначаемое A∪B, есть множество элементов, содержащихся в множестве А, в множестве В или в обоих множествах А и В.

Объединение множеств А и Т есть множество всех вещественных чисел R. Следовательно, можно написать R = A∪T.

А теперь приготовьтесь к поворотному моменту этой истории. Поскольку мощность R, множества всех вещественных чисел, равна А, можно предположить, что множество Т должно быть несчетным (или меньше).

Утверждение о том, что множество трансцендентных чисел Т должно быть несчетным, вытекает из того факта, что объединение двух счетных множеств всегда дает еще одно счетное множество.

Если бы оба множества А и Т были счетными – то есть счетными были бы и множество алгебраических чисел, и множество трансцендентных чисел, – то их элементы можно было бы упорядочить: A = ( a 1, a 2, a 3…) и T = ( t 1, t 2, t 3…). Следовательно, их объединение T∪A тоже было бы счетным, так как его элементы можно было бы упорядочить следующим образом:

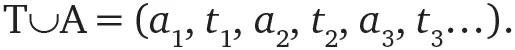
Но, как мы знаем, множество R несчетно. Поскольку нам известно, что множество А счетно (см. раздел под названием «Каникулы алгебраических чисел в отеле Гильберта»), а T∪A = R, множество Т никак не может быть счетным.

Что же, если количество трансцендентных чисел так велико, что они образуют несчетное множество, казалось бы, найти пример трансцендентного числа должно быть совсем не трудно. Да что там, математики должны то и дело на них натыкаться.

Но так ли это? На самом деле нет. Даже к нынешнему моменту выявлено очень немного трансцендентных чисел.

Давайте попробуем. Может быть, трансцендентно число (√2 + ϕ)? Ничего подобного. Это число оказывается алгебраическим: можете попытаться составить алгебраическое (полиномиальное) уравнение (с целыми коэффициентами), решением которого оно является. Собственно говоря, готов поспорить, что вы не сможете найти ни одного неалгебраического числа.

Что же получается? Мы доказали, что количество трансцендентных чисел не просто бесконечно, но и несчетно. Проблема состоит в том, что это доказательство существования, а не конструктивное доказательство. Другими словами, хотя это доказательство может убедить нас в существовании бесконечно многих трансцендентных чисел (что вытекает из мощности континуума), оно не дает ни малейшей подсказки относительно того, как найти хотя бы одно такое число.

Как мы уже сказали, в 1844 г. Лиувилль открыл одно трансцендентное число. Вот оно:

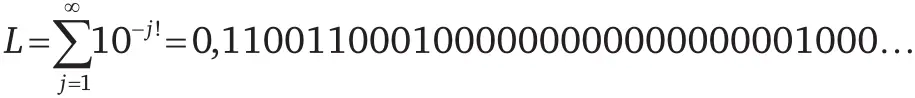
Вам может быть не вполне ясно, что именно это за число; позвольте мне объяснить.

Число Лиувилля строится следующим образом:

Шаг 1. Вычисляем все факториалы: 1! = 1, 2! = 2, 3! = 6, 4! = 24, 5! = 120…

Шаг 2. Составляем число, в котором после запятой встречаются только нули и единицы, причем 1 стоит на 1-м, 2-м, 6-м, 24-м, 120-м – и так далее – местах, а на всех остальных местах стоит 0.

Лиувилль доказал, что это число не является корнем какого бы то ни было алгебраического уравнения с целыми коэффициентами.

Как вы можете вообразить, это доказательство не слишком просто, так что вам придется поверить мне (и Лиувиллю) на слово – это действительно так.

Посмотрите на следующее число: 3,140001000000000000000005… сформированное сходным образом. Это число получено из десятичного представления числа π, в котором все цифры после запятой, кроме 1-й, 2-й, 6-й, 24-й, 120-й и так далее (их номера соответствуют 1! 2! 3!..), заменены нулями. На упомянутых же местах стоят последовательные цифры числа π.