Хаим Шапира - Восемь этюдов о бесконечности. Математическое приключение

Вот расположение слов:

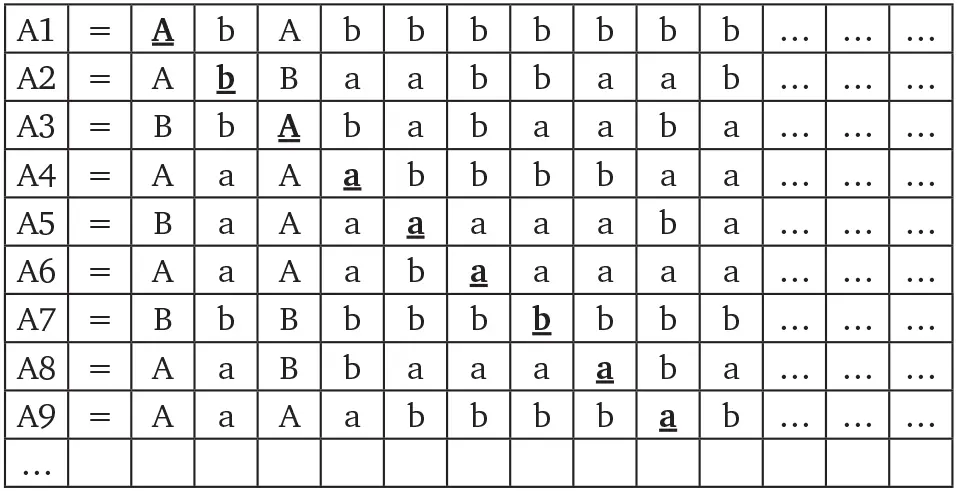
Применяя диагональный метод Кантора, аналогично тому, как мы действовали с числами, заключенными между 0 и 1, образуем новое слово А0, которое не содержится где бы то ни было в представленном в таблице множестве, в каком бы порядке мы ни располагали слова. Внимательно посмотрите на таблицу и обратите внимание на подчеркнутые буквы, стоящие на диагонали. Новое слово А0 будет построено следующим образом: его первая буква будет отличной от первой буквы слова А1 (поскольку первая буква в А1 – а, мы возьмем букву b); вторая буква будет отличной от второй буквы слова А2 (раз это буква b, мы используем букву а); третья буква будет отличной от третьей буквы слова А3 (на этот раз возьмем букву b) – и так далее.

Итак, наше новое слово A0 = babbbbabb…

Я предоставлю умудренному читателю самостоятельно убедиться, что слово А0 никоим образом не может встретиться в исходном бесконечном списке (то есть совпасть с каким бы то ни было его словом), потому что оно не может не отличаться от любого слова A i по меньшей мере буквой, стоящей на i -м месте.

К тому же, как уже выяснила Омега, добавление слова А0 в список ничего не меняет, потому что мы всегда можем повторить ту же процедуру и построить еще одно слово, назовем его Aℵ, которое будет отличаться от всех без исключения слов, включенных в составленный нами бесконечный список. Итак, множество всех слов бесконечной длины, содержащих только буквы a и b, имеет мощность континуума.

Очевидно, множество всех слов бесконечной длины, составленных с использованием трех разных букв (а не только букв a и b) или четырех или пяти (или любого другого количества) разных букв, также должно иметь мощность несчетного множества, что само по себе не означает, что его мощность будет равна мощности континуума. Однако, поскольку мы можем построить между таким множеством и множеством чисел, составленных из 0 и 1, одно-однозначное и сюръективное отображение, мы видим, что его мощность действительно равна ℵ.

Предположим, что верна противоположная гипотеза: все точки отрезка [0,1] можно пересчитать. Из этого следует, что все эти точки можно расположить в некотором последовательном порядке – {p 1, p 2, p 3, p 4…}. Чтобы доказать (или опровергнуть) эту гипотезу, возьмем вокруг центральной точки p 1отрезок длиной, скажем, 1/10, вокруг точки p 2 – отрезок длиной 1/100, вокруг точки p 3 – отрезок длиной 1/1000 и так далее. Поскольку все точки, содержащиеся на отрезке [0,1], попадают по меньшей мере на один из этих отрезков (вспомним, что в множестве {p 1, p 2, p 3, p 4…} были перечислены все числа, расположенные между 0 и 1), мы получаем множество, покрывающее весь отрезок [0,1]. А также можно сложить длины всех этих отрезков. В соответствии с формулой для бесконечной геометрической прогрессии:

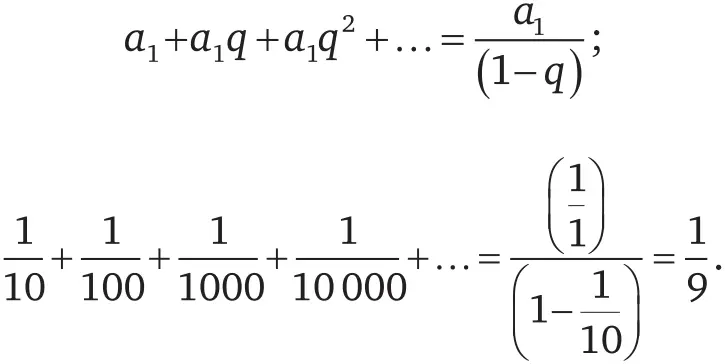
Нам удалось, так сказать, покрыть все точки отрезка числовой прямой [0,1] интервалами, суммарная длина которых составляет всего лишь 1/9. Но это, очевидно, невозможно, так как длина исходного отрезка числовой прямой равна 1.

Таким образом, мы пришли к противоречию.

Вывод: Составить последовательность из всех точек, находящихся между 0 и 1, невозможно. Другими словами, это множество несчетно.

Поскольку рациональные числа образуют счетное множество, все рациональные числа, содержащиеся на отрезке [0,1], можно обработать определенным образом. Как? Окружая их отрезками так, чтобы суммарная длина этих отрезков не превышала 1/9. Из этого следует, что рациональные числа в сумме составляют не более 1/9 всех чисел, существующих между 0 и 1.

Однако этот верхний предел можно уточнить.

Предположим теперь, что рациональные числа, находящиеся на отрезке [0,1], располагаются следующим образом: {q 1, q 2, q 3, q 4…}. Возьмем вокруг точки q 1интервал длиной 1/1000, вокруг точки q 2 – интервал длиной 1/10 000, вокруг точки q 3 – интервал длиной 1/100 000 и так далее. Тогда суммарная длина всех таких интервалов будет равна

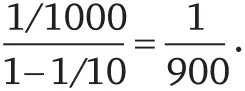
Очевидно, длину суммарного интервала, охватывающего все рациональные числа на отрезке [0,1], можно уменьшать и дальше, получая эту суммарную длину сколь угодно малой. Множество, которое покрывается счетным объединением интервалов, суммарная длина которых меньше любого заранее определенного значения, называется множеством нулевой меры.

Все истинные положения легко понять после того, как они найдены; суть в том, чтобы их найти [51] «Диалог о двух главнейших системах мира» (1632). День второй. Пер. С. Н. Долгова. .

Математика – самое прекрасное и самое могущественное произведение человеческого духа.

Как я уже отмечал, мощность множества всех вещественных чисел – как рациональных, так и иррациональных, – расположенных между 0 и 1, обозначается символом ℵ и называется мощностью континуума. В отрезке от 0 до 1 нет ничего особенного. Его длина равна единице, но мощность любого другого отрезка – тоже ℵ. Легко видеть, что любые два отрезка равномощны, то есть существует одно-однозначное и сюръективное соответствие между любым отрезком AB и множеством точек другого отрезка, CD. Наглядно представить такое соответствие поможет следующая подсказка:

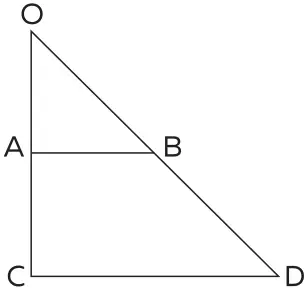
Подсказка не помогла? Тогда вот решение. Как показано на приведенном ниже чертеже, для каждой точки на отрезке АВ можно найти соответствующую ей точку на отрезке CD.

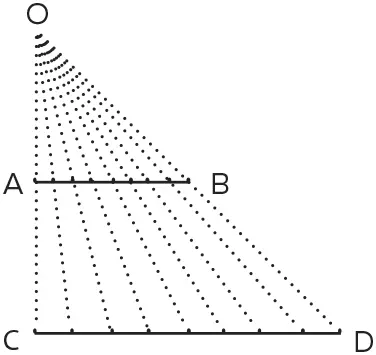
Ясно, что каждая конкретная точка более короткого отрезка, АВ, может быть соединена с разными точками отрезка CD. Получается одно-однозначное соответствие.

Так же ясно, что для каждой точки отрезка CD можно найти соответствующую ей точку отрезка АВ. Для этого нужно всего лишь провести прямую, соединяющую точку на отрезке CD с вершиной треугольника, и найти точку ее пересечения с отрезком AB. Это дает сюръективное соответствие.

Поскольку нам удалось образовать пары из всех точек двух отрезков разной длины, значит, они должны иметь одинаковую мощность – следовательно, мощность континуума, то есть ℵ.