Хаим Шапира - Восемь этюдов о бесконечности. Математическое приключение

С годами стало ясно, что вопросы о бесконечности должны быть очень близки к самым основам математики, и подходить к ним следует с чрезвычайной осторожностью.

В 1908 г. был создан набор аксиом, который называется системой Цермело – Френкеля (ZF). Мы уже знакомы с Цермело (это он защищал Кантора и сформулировал первую теорему теории игр); Абрахам Галеви Френкель был израильским математиком, ставшим первым деканом Математического факультета Еврейского университета в Иерусалиме. Они сформулировали свою систему, чтобы создать для теории множеств – и математики в целом – надежную основу, которая дала бы математикам строгие методы для работы с бесконечными множествами и решения некоторых задач в этой области – например парадокса Рассела. Аксиомы ZF – это попросту в высшей степени элементарные утверждения о концепции множеств, которые, как мы верим (да, верим всем сердцем!), настолько самоочевидны, что не вызывают сомнений. Вот, например, «аксиома пустого множества»:

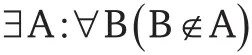
В переводе на человеческий язык это означает «существует множество, не содержащее элементов» [54] Точнее говоря, это выражение читается так: «Существует такое А, что для любого В верно, что В не принадлежит А». .

Предполагалось, что аксиоматическая система будет играть в теории множеств ту же роль, которую играет в геометрии система аксиом Евклида. Однако на деле вышло не совсем так.

В 1938 г. австрийский логик, математик и философ Курт Гёдель доказал, что континуум-гипотезу невозможно опровергнуть , используя аксиоматическую систему Цермело – Френкеля для теории множеств. 25 лет спустя, в 1963 г., Пол Коэн (1934–2007), профессор математики из Стэнфордского университета, продемонстрировал невозможность доказательства континуум-гипотезы на основе аксиом Цермело – Френкеля. Коэн и Гёдель доказали, что континуум-гипотезу невозможно ни доказать, ни опровергнуть. В результате оказалось, что вопрос об истинности континуум-гипотезы не может быть решен исходя только из аксиом ZF. Так явилось на свет первое «неразрешимое» утверждение.

В старом Евклидовом мире действовала Аристотелева логика, предполагавшая лишь два варианта правильности утверждения: оно могло быть либо истинным (Т), либо ложным (F). Теперь у нас появился третий вариант: утверждение может быть неразрешимым (U) [55] T – сокр. англ. true («истинный»), F – false («ложный»), U – undecidable («неразрешимый»). .

Очевидно, можно спросить: не вызвана ли эта проблема с неразрешимыми утверждениями тем, что в системе Цермело – Френкеля не хватает каких-нибудь аксиом? Вполне может быть так, что существует еще одна «очевидно истинная» концепция, пока не открытая, добавление которой к системе ZF позволит доказать СН. Или, если рассматривать этот вопрос с еще более оптимистической точки зрения, можно ли усовершенствовать ZF какими-нибудь дополнительными аксиомами так, чтобы все утверждения стали разрешимыми в этой системе?

В 1931 г. Гёдель, которому было тогда всего 25 лет, выдвинул три теоремы – одну о полноте и две о неполноте, – которые рассматривают общий случай неразрешимых утверждений. Суть первой теоремы о неполноте сводится к тому, что в какой бы системе аксиом мы ни работали, если эта система достаточно развита, чтобы порождать натуральные числа, в ней всегда существуют неразрешимые утверждения {32} 32 У такой системы должны быть и другие естественные свойства, которыми обладает система ZF. . Такое ограничение того, чего можно было бы ожидать от аксиоматической системы, было непредвиденным.

Эти три теоремы настолько потрясли математический мир, что споры о их сути продолжаются и по сей день. Эта интереснейшая тема, несомненно, заслуживает отдельного рассмотрения.

На протяжении более чем полувека математики, работающие в области аксиоматической теории множеств, пытались найти «недостающую аксиому» (или аксиомы). Успеха никто из них не добился. Сейчас большинство специалистов в этой области считают, что никаких недостающих аксиом нет, и правильный подход к этому вопросу заключается в рассмотрении взаимосвязей между разными аксиомами. Можно, конечно, принять за аксиому саму континуум-гипотезу, но тут важно помнить, что аксиомы должны быть сформулированы так, чтобы в их справедливость было легко поверить, а в случае континуум-гипотезы это требование явно не выполняется.

В 2006 г. (за год до смерти) Пол Коэн прочитал интереснейшую лекцию о континуум-гипотезе на конференции в честь Гёделя, проходившей в Вене. Его лекцию (в шести частях) можно найти на YouTube по запросу: Paul Cohen part 1 of 6, Centennial, Vienna.

Тем временем в геометрии восстали из пепла некоторые интересные теории относительно невозможности обоснования пятого постулата при помощи евклидовой аксиоматической системы. В XIX в. были разработаны две другие геометрические системы, которые считаются неевклидовыми геометриями. Первая из них (гиперболическая геометрия [56] Она же геометрия Лобачевского. ) предполагает, что через точку А , не лежащую на прямой m , можно провести более одной прямой, не пересекающей прямую m . Вторая (эллиптическая геометрия [57] Она же геометрия Римана. ) предполагает, что через точку А, не лежащую на прямой m, невозможно провести ни одну прямую, не пересекающую прямую m .

Подобно тому, как попытки обоснования пятого постулата в евклидовой геометрии привели к появлению в геометрии новых, неевклидовых теорий, обоснование континуум-гипотезы также дало толчок развитию неканторовой теории множеств, не предполагающей континуум-гипотезы. Честно говоря, неканторовых теорий существует много, потому что в последние годы математики, применяя предложенный Полом Коэном систематический метод «форсинга», доказали неразрешимость многих еще не решенных классических открытых проблем.

В прошлом можно было считать, что любое математическое утверждение может быть либо доказано, либо опровергнуто – если только над ним будут достаточно долго работать достаточно умные математики. Теоремы Гёделя доказали, что существуют утверждения не истинные и в то же время не ложные. Они, собственно говоря, неразрешимы.

Математику можно определить как область, в которой мы никогда не знаем, ни о чем мы говорим, ни истинно ли то, что мы говорим.

Парадокс, о котором мы сейчас будем говорить, носит имя французского математика Жюля Ришара (1882–1956) и был опубликован в 1905 г. Ниже я даю словесное (а не формальное) описание этого парадокса.