Хаим Шапира - Восемь этюдов о бесконечности. Математическое приключение

Доказательство того, что булеан множества, содержащего n элементов, содержит 2 n подмножеств, получено при поддержке Уильяма Шекспира и состоит в следующем: каждый элемент исходного множества должен решить, «быть или не быть» элементом каждого конкретного подмножества. Следовательно, поскольку у каждого элемента есть две возможности относительно каждого отдельного подмножества, суммарное число возможностей для n элементов равно 2 n .

Чтобы пояснить эту концепцию на конкретном примере, предположим, что мы набираем подмножество из элементов множества A = {17, 42, 0}. 17 и 0 «решают» стать элементами этого подмножества, а 42 отказывается. В сочетании эти решения дают подмножество {17, 0}. Решения каждого из элементов множества однозначно определяет состав каждого конкретного подмножества; следовательно, количество подмножеств равно количеству уникальных решений, то есть 2 × 2 × 2 × … × 2 = 2 n .

Ч. т. д.

Мощность любого множества А строго меньше, чем мощность P(A).

Попросту говоря, теорема Кантора означает, что «количество» элементов множества А, то есть #A, должно быть строго меньше, чем «количество» подмножеств в соответствующем булеане, P(A). Другими словами, булеан любого множества должен иметь бо́льшую мощность, чем само это множество.

Теперь возьмем бесконечное множество, например счетное множество с мощностью ℵ 0или континуальное множество с мощностью ℵ. Мощность их булеанов обозначается соответственно

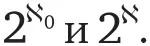
1. Докажите теорему Кантора (подсказка: парадокс Рассела).

2. Поскольку мощность множества натуральных чисел равна ℵ 0, мощность множества его подмножеств должна быть

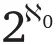
Докажите, что

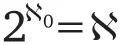
Другими словами, докажите, что мощность всех подмножеств множества натуральных чисел равна мощности континуума.

В 1897 г. итальянский математик Чезаре Бурали-Форти представил парадокс, который впоследствии стал называться его именем. Его можно описать следующим образом.

Рассмотрим множество всех множеств, то есть включающее в себя множество всех живущих ныне людей, множество всех людей, которые жили в прошлом, множество всех песен, которые можно сочинить, множество всех женщин, которых никогда не показывали на Fashion Channel [60] World Fashion Channel – международный телеканал, вещающий о современных тенденциях в моде, красоте, путешествиях, технологиях и стиле жизни. – Примеч. ред. , множество всех женщин, которых зовут Гризельда, множество всех цветов, множество всех идей, о которых никто никогда не сможет подумать, множество всех сражений, в которых я не участвовал, множество всех вещественных чисел, множество всех кинофильмов, которые не поставил Тарковский, множество всех кинофильмов, которые можно или можно было посмотреть на сайте YouTube, множество всех функций, множество всех философов, которые никогда не страдали от депрессии, множество всех молекул, которые находятся в данный момент в подвале моего дома… Теперь прибавим к нему все подмножества всех множеств. Короче говоря, пусть в этом множестве множеств содержится все, о чем только можно помыслить.

Обозначим это множество множеств Ω.

Очевидно, мощность Ω должна быть больше, чем мощность любого другого множества, – потому что оно включает в себя всё на свете. Но теорема Кантора утверждает, что #P(Ω) > #(Ω). То есть мощность P(Ω) больше, чем мощность Ω, множества всех множеств!

Кантора этот парадокс не особенно обеспокоил, так как он считал, что множество всех множеств слишком велико, чтобы считать его множеством. Не должен удивлять и читателя этой книги, так как мы знаем в свете парадокса Рассела, что не всякий набор объектов образует правильное множество.

Надеюсь, теперь вам ясно, что термины «мощность» или «кардинальное число» – это просто обобщение концепции «количества элементов», применяемой для конечных множеств, на множества бесконечные. Количество элементов конечных множеств обозначается натуральными кардинальными числами , но интуитивно понятно, что кардинальные числа также определяют количество элементов в бесконечных множествах. Например, если мощность некоторого множества – ℵ 0, то в нем содержится такое же количество элементов, как и в множестве натуральных чисел.

На уроках математики мы заучили, что над конечными числами можно производить математические операции – например сложение, деление и умножение. Такие же базовые операции можно определить и для множеств. В самом деле, когда мы складываем два натуральных числа, мы, по сути дела, «объединяем» их; эта операция аналогична объединению двух непересекающихся множеств (непересекающимися называются множества, не имеющие общих элементов). Если в одном множестве m элементов, а в другом – n элементов, то объединение этих двух множеств будет содержать n + m элементов.

Приведем один простой пример:

Если A = {Q, W, E, R, T, Y}, а B = {17, 21}, то A∪B = {Q, W, E, R, T, Y, 17, 21}.

В этом случае #A = 6, а #B = 2; следовательно, #A∪B = 6 + 2 = 8.

Операции с кардинальными числами работают точно так же. Например, чтобы вычислить сумму ℵ 0 + ℵ 0, нужно взять два непересекающихся множества, причем оба они должны быть счетными, и посмотреть, какую мощность будет иметь их объединение. Из приведенного примера мы увидим, что результат не зависит от того, какие именно множества мы выберем.

Например, возьмем A = (1, 3, 5, 7, 9, 11…) и B = (2, 4, 6, 8, 10…). Множества А и В не пересекаются, а мощность каждого из них, разумеется, равна ℵ 0.

Как вы видите, A∪B = N, то есть их объединение дает множество всех натуральных чисел, мощность которого, как мы знаем, равна ℵ 0.

Итак, получается, что ℵ 0 + ℵ 0 = ℵ 0. Собственно говоря, мы не открыли ничего нового: мы уже знали, что объединение двух счетных множеств также является счетным множеством.

Но тут нужна осторожность! Не следует увлекаться и думать, что к бесконечным значениям можно применять все правила обычной математики. Например, хотя ℵ 0 + ℵ 0 = ℵ 0, мы не можем вычесть из обеих частей этого равенства по ℵ 0, потому что тогда мы получили бы бессмысленное и, честно говоря, довольно нелепое выражение ℵ 0 = 0! Поэтому следует помнить, что обращение с бесконечными значениями требует некоторой осмотрительности.