Хаим Шапира - Восемь этюдов о бесконечности. Математическое приключение

Этот факт весьма удивителен, так как множество Кантора не имеет никакой длины. Действительно, сумма длин всех отрезков, которые мы удаляем, равна:

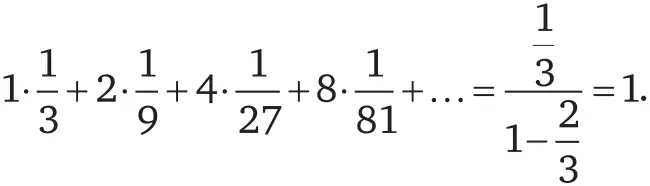
Таким образом, длина множества Кантора есть результат вычитания из 1 суммарной длины всех этих отрезков, то есть 1, а следовательно, длина множества Кантора равна 0.

Множество Кантора – действительно очень необычный объект. Оно содержит невычислимое количество точек – суммарная длина которых равна нулю! – которые находятся на множестве отрезков прямой! Кроме того, множество Кантора считают первым фракталом. Но этой теме придется подождать другой книги.

Между прочим, число 1 можно записать в троичном представлении как 0,2222… а в десятичном – как 0,999999… Когда я пишу, что 1 = 0,999999… многие удивленно поднимают бровь (или даже обе). Они пытаются объяснить мне, что это неверно, что 1 хоть совсем ненамного, но все же больше, чем 0,999999…

Чаще всего бывает почти невозможно убедить кого-нибудь в моей правоте. Но это не значит, что я не попытаюсь это сделать.

Попробуйте вычесть 0,9999… из 1. Что у вас получается? Если ваш результат хоть на сколько-нибудь отличается от нуля, значит, вы совершаете логическую ошибку.

Или же попробуем сделать вот что. Пусть a = 0,9999999… В таком случае 10 a = 9,999999… Вычтя одно число из другого, получим 10 a – a = 9,999999… – 0,999999… А это превосходным образом дает 9 a = 9, то есть a = 1.

Если уж и это вас не убедило, мне очень жаль.

У книги о бесконечности не может быть конца; бесконечность – это нескончаемая история. Поэтому я не стану писать заключения, а дам вам одну очень красивую задачу, и вы сможете обдумывать ее столько, сколько захотите.

Взгляните на следующее равенство:

1/9801 =0,00010203040506070809101112131415161718192021

2223242526272829303132333435363738394041424344

4546474849505152535455565758596061626364656667

6869707172737475767778798081828384858687888990

919293949596979900010203…979900010203…

Видите, что тут происходит?

Не видите?

Ну хорошо.

Вот вам то же самое, но в лучшем разрешении:

1/9801 =0,00 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21

22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46

47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71

72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96

97 99 00 01 02 03…97 99 00 01 02 03 04 05 06… ad infinitum [61] До бесконечности ( лат .). .

Мы получили все двузначные числа, расположенные в правильном порядке (!) и повторяющиеся до бесконечности, кроме числа 98.

Почему отсутствует число 98?

Действительно ли отсутствует число 98?

Что получится, если рассмотреть 1/1089?

Что получится, если рассмотреть 1/998 001?

А завершу я текст этой книги своим любимым словом:

ПОЧЕМУ?

Прежде всего я хотел бы поблагодарить Итана Ильфельда за веру в меня и в мои книги.

Я хотел бы воздать благодарность моей верной переводчице Линде Иехиэль.

Я хотел бы выразить особую признательность Алену Деккеру, никогда не перестававшему спорить со мной, за огромную помощь и терпение.

Я чрезвычайно благодарен Тому Бенаму, специалисту по теории множеств, за мудрое редактирование моей книги и множество блестящих идей.

Кроме того, я хотел бы поблагодарить ответственного за издание этой книги, Слава Тодорова, и выразить свою признательность всем сотрудникам издательства Watkins, работавшим над ней.

Наконец, но ни в коем случае не в последнюю очередь, я хотел бы поблагодарить своих агентов – Вики Сатлоу и Зива Льюиса.

Для тех, кто хотел бы изучить этот предмет поглубже, ниже приводится очень краткий список некоторых из тех книг, которые, по моему мнению, стоит прочитать.

Marcus du Sautoy. The Music of the Primes.

George Gamow . One Two Three… Infinity.

Martin Gardner. The Colossal Book of Short Puzzles and Problems.

Raymond Smullyan. Satan, Cantor and Infinity ( Смаллиан Р. Сатана, Кантор и бесконечность, а также другие головоломки / Пер. с англ. П. И. Быстрова. М.: Лори, 2014).

Douglas Hofstadter. Gödel, Escher, Bach (Хофштадтер Д. Гёдель, Эшер, Бах: эта бесконечная гирлянда / Пер. с англ. М. А. Эскиной. Самара: Издательский дом «Бахрах-М», 2001).

G. H. Hardy. A Mathematician’s Apology ( Харди Г. Г. Апология математика / Пер. с англ. Ю. А. Данилова. Ижевск: НИЦ «Регулярная и хаотическая динамика», 2000).

Хаим Шапирародился в 1962 г. в Литве. В 1977 г. он эмигрировал в Израиль, где получил первую докторскую степень по математической генетике за диссертацию по теории игр и вторую – за исследование математических и философских аспектов изучения бесконечности. Сейчас преподает математику, психологию, философию и литературоведение. Его перу принадлежат книги, ставшие бестселлерами. В своих сочинениях он пытается не склонить читателя к своей точке зрения, а побудить его мыслить самостоятельно. Хаим Шапира стал одним из наиболее популярных и востребованных лекторов в Израиле и говорит в своих выступлениях о творчестве и стратегическом мышлении, об экзистенциальной философии и философии в детской литературе, о счастье и оптимизме, о бессмыслице и безумии, о воображении и смысле смысла, а также о любви и дружбе. Кроме того, он превосходный пианист и заядлый коллекционер всего прекрасного.

«Беседы и математические доказательства, касающиеся двух новых отраслей науки». День первый. (Пер. С. Н. Долгова.) Здесь и далее цит. по: Галилей Г. Избранные произведения: В 2 т. М.: Наука, 1964. Т. 2.

Китайское название – «Лунь юй», первая из четырех книг конфуцианского канона. В русских переводах называется также «Беседы и суждения». – Здесь и далее, если не указано иное, постраничные примеч. перев.

Более того, даже кажущееся сходство названий этих игр случайно. Го моку означает по-японски «пять камней». Название же игры го происходит от слов и-го, японского перевода китайского названия вэй-ци , которое традиционно переводится на русский как «облавные шашки».

«Две новые науки». День первый.

Здесь и далее цит. по: Паскаль Б. Мысли / Пер. с фр. Ю. А. Гинзбург. М.: Изд-во имени Сабашниковых, 1995.

Звукоподражательное слово, передающее чавканье. Дело в том, что в эту игру можно играть на разделенной на дольки плитке шоколада: игрок, делающий очередной ход, отламывает и съедает те «клетки», которые он занимает по правилам игры. В русском варианте ( Гарднер М. Математические новеллы / Пер. с англ. Ю. А. Данилова. М.: Мир, 1974) игра называется «Щелк!».