Хаим Шапира - Восемь этюдов о бесконечности. Математическое приключение

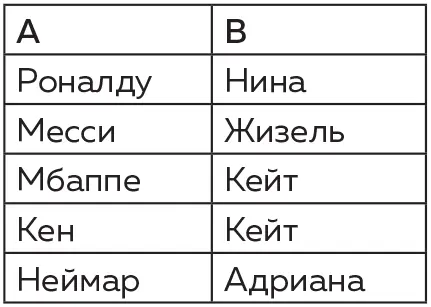
Это соответствие сюръективно, потому что каждый из элементов множества В (четырех манекенщиц) образует пару по меньшей мере с одним элементом множества А (футболистом). Заметим, что в этом случае два футболиста «отображаются на» одну из манекенщиц (Кейт). В то же время следующее соответствие не будет сюръективным:

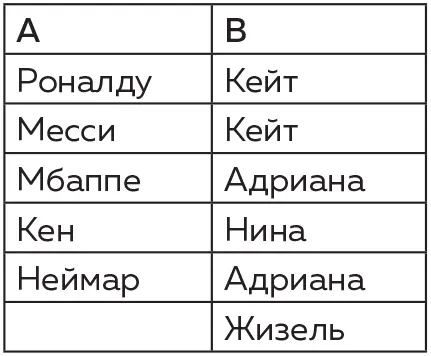
Почему? Потому что один из элементов множества В (Жизель) не образует пары ни с одним из элементов множества А. Обратите внимание, что на двух манекенщиц «отображаются» по два футболиста, в результате чего бедная Жизель остается в одиночестве.

Если между двумя множествами А и В существует и одно-однозначное, и сюръективное соответствие, это означает, что элементы этих множеств могут быть разбиты на «идеальные» пары – каждому индивидуальному элементу множества А может быть сопоставлен элемент множества В, а каждому элементу множества В может быть сопоставлен элемент множества А. Соответствие, которое является одновременно инъективным и сюръективным, называется биективным [46] Или взаимно-однозначным. .

Совершенно ясно, что, если оба множества А и В конечны, то существование между ними и одно-однозначного, и сюръективного соответствий возможно, только если оба множества содержат одинаковое количество элементов. Поясню: наличие одно-однозначного (инъективного) соответствия означает, что количество элементов множества В равно количеству элементов множества А или больше его, а наличие сюръективного соответствия предполагает, что большее или равное число элементов содержит множество А (поскольку каждый элемент множества В может быть связан с несколькими элементами множества А). В сочетании эти два условия означают, что, если А и В – конечные множества, то количество элементов в них должно быть одинаковым.

Можно продемонстрировать, что соответствие между множеством футболистов и множеством манекенщиц является одновременно одно-однозначным и сюръективным тогда, и только тогда, когда оба эти множества содержат одно и то же количество элементов, как в следующем примере (приведенном для тех, кто тоскует по прошлому):

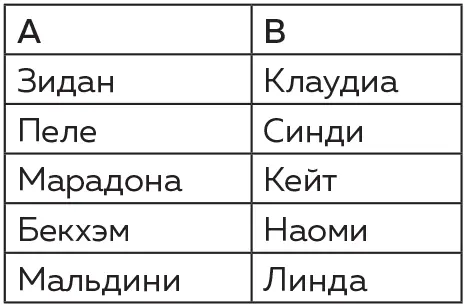
Вот еще один пример:

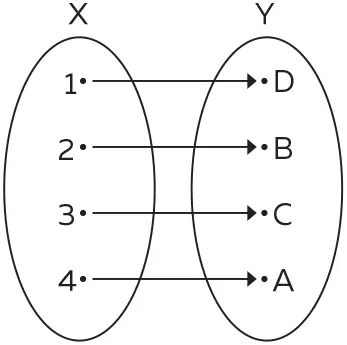
В нем также имеются одно-однозначное и сюръективное соответствие, и нам даже не пришлось привлекать футболистов или манекенщиц.

Теперь, прояснив все эти вопросы, вернемся к бесконечным множествам. Исходя из изложенного выше, кажется естественным дать следующее определение равенства количества элементов двух множеств (будь то конечных или бесконечных):

Два множества А и В имеют равную мощность, если между элементами множества А и элементами множества В существует некоторое (любое) соответствие, одновременно одно-однозначное (инъективное) и сюръективное.

Что же это за «мощность»? Возможно, вы помните, что мы уже упоминали ее некоторое время назад. Смысл мощности конечных множеств вполне ясен.

В случае конечных множеств мощность – это просто вычурное обозначение «количества элементов множества». Например, множество A = {17, 42, 1729, 1 234 321} содержит четыре элемента; следовательно, его мощность (которую называют также кардинальным числом) равна 4. Это утверждение можно записать следующим образом: #A = 4 [47] В русской математической литературе чаще используется другое обозначение мощности: |А|. Есть и другие варианты: А= или card(A). Мы будем использовать символ #, как это делает автор книги. .

Однако в случае бесконечных множеств понятие «количества элементов множества» не очевидно и не может быть очевидно. Когда речь идет о бесконечных множествах, мы можем только сравнивать их мощности.

В начале XVII в. Галилео Галилей описал парадокс, который был назван его именем. В парадоксе Галилея речь идет об одно-однозначном и сюръективном соответствиях между множеством натуральных чисел {1, 2, 3, 4…} и множеством полных квадратов {1, 2, 4, 9, 16…}. Из элементов этих множеств можно составить пары, как показано в приведенной ниже таблице. Должно быть очевидно, что для каждого элемента множества А существует один, и только один, соответствующий ему элемент множества В, и наоборот:

Возникающий здесь парадокс состоит в том, что множество натуральных чисел и его собственное подмножество – то есть подмножество, не равное самому этому множеству [48] А также не являющееся пустым множеством, но это сейчас не важно. , в данном случае множество полных квадратов, – имеют одинаковую мощность (то есть между ними существует одно-однозначное и сюръективное соответствие). Как такое может быть, если натуральных чисел больше, чем квадратов, то есть в одном множестве должно быть больше элементов, чем в другом? Как же они могут быть равномощными?!

Георг Кантор

© Morphart Creation / Shutterstock.com

Галилео Галилей

© Morphart Creation / Shutterstock.com

Положение или предположение, противоречащее общепринятому мнению; утверждение или ощущение, кажущееся противоречивым или идущим вразрез со здравым смыслом; нечто выглядящее или представленное абсурдным, но могущее быть истинным.

Как замечательно, что мы столкнулись с парадоксом! Теперь у нас есть надежда чего-нибудь добиться.

Как я согласен с Нильсом Бором! Парадоксы прекрасно помогают как следует встряхнуть процесс размышлений.

Галилей считал, что этот парадокс, о котором он писал в «Беседах о двух новых науках» (Discorsi e dimostrazioni matematiche intorno a due nuovi scienze attenenti alla mecanica e i movimenti locali, 1638), доказывает, что в разговоре о бесконечных множествах нельзя использовать прилагательные вроде «равный», «больший» или «меньший»; более того, как мы уже упоминали гораздо раньше в этой книге, существам с конечным разумом вообще лучше держаться подальше от всего того, что касается бесконечности.