Хаим Шапира - Восемь этюдов о бесконечности. Математическое приключение

– Что?! – Администратор гостиницы не поверила своим ушам.

– Все номера, не соответствующие простым числам или степеням простых чисел, – например 1, 6, 10, 12, 14, 15, 18… – остаются совершенно пустыми.

Администратор, лишь мгновением раньше бывшая в восторге от того блестящего метода, который предложил для решения проблемы расселения профессор, снова впала в полнейшее отчаяние. Перед ней снова возникла проблема уровня заполненности гостиницы. Хороший администратор гостиницы просто не может позволить себе иметь бесконечно много (!) незанятых номеров. Что подумают хозяева гостиницы?

– Послушайте, – сказала Омега профессору, – одни только натуральные числа могут заполнить всю гостиницу, и так оно раньше и было. А теперь вы предлагаете какую-то безумную схему, по которой натуральные числа вместе с бесконечным количеством других бесконечных множеств, каждое из которых тоже могло бы заселить всю гостиницу, создают мне уровень заполненности гораздо ниже 100 процентов. По-моему, в этом нет никакой логики. Я, конечно, не специалист, но нет ли какого-нибудь способа, который позволил бы мне отчитаться начальству о значительно более высокой заполненности гостиницы?

– Что же, я думал, что решение будет гораздо более эффектным, если останется бесконечное число незанятых номеров. Но если вас интересует только уровень заполненности, я могу предложить другой вариант, в котором все номера будут заполнены на 100 процентов.

– Пожалуйста, расскажите мне о нем! – взмолилась Омега.

– Прежде чем я объясню это решение, нам нужно провести небольшую подготовку. Поставим в соответствие каждому рациональному числу пару чисел. Первым из них будет его числитель, а вторым – знаменатель. Например, числу 3/4 будет соответствовать пара чисел (3, 4). Каждое натуральное число n мы будем записывать в виде дроби n /1; тогда ему будет соответствовать пара ( n , 1). Например, числу 7 соответствует пара (7, 1). Теперь расположим все эти числа следующим образом:

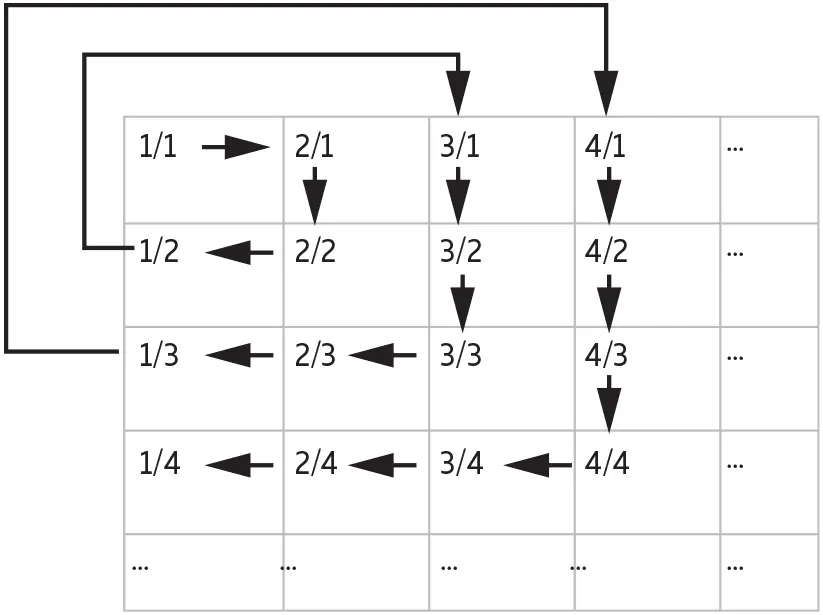
Отмечу для любителей алгебры, что в общем случае мы выделяем числу n / m номер n ² – m + 1, если n ≥ m , и номер ( m – 1)² + n , если n < m .

Например, у числа 3/2 числитель больше знаменателя; следовательно, ему должен быть предоставлен номер 3² – 2 + 1, то есть номер 8. Можете убедиться сами: если начать с пары (1, 1) и следовать по стрелкам (см. приведенный выше чертеж), то клетка с парой (3, 2) будет восьмой на этом пути.

Администратор была вне себя от счастья. Она даже запустила новую рекламную кампанию под лозунгом «Мы бесконечно рады всем!».

Профессор Финкельштейн-Островский-Канторович отметил, что существует огромное количество разных способов расселения в гостинице рациональных чисел:

– Вот один из этих способов. Определим для каждой дроби n / m «высоту», равную сумме числителя и знаменателя этой дроби. Другими словами, пусть высота h дроби n / m равна n + m . Наименьшая такая высота равна 2, причем есть только одна дробь с такой высотой – а именно 1/1. Есть два рациональных числа, высота которых равна 3; это числа 1/2 и 2/1. У чисел 1/3, 2/2 и 3/1 высота h = 4, а таких чисел, для которых h = 5, существует четыре: 1/4, 2/3, 2/3, 4/1. Таким образом, все рациональные числа можно расположить в порядке возрастания их высоты {28} 28 Числа с равной высотой располагаются в порядке возрастания числителя. .

Докажите, что по предложенной выше схеме расселения число n / m будет жить в номере, соответствующем выражению ½ · ( n + m – 2) ( n + m – 1) + n .

Например, число 2/3 ( n = 2, m = 3) окажется в номере ½ · (2 + 3 – 2) (2 + 3 – 1) + 2 = 8.

Подсказка:

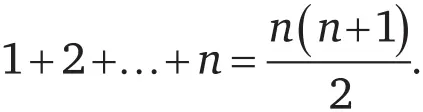
Слава о гостинице, которая способна разместить любую группу постояльцев, широко разошлась. Не имело значения, какая приезжала группа, конечная или бесконечная; не имело значения, были ли уже в гостинице другие жильцы; даже не имело значения, были ли все номера в гостинице уже забронированы. Как только приезжала новая группа постояльцев, им всем можно было найти место.

Но однажды случилось нечто, чего Омега совершенно не ожидала. Утром этого дня по электронной почте пришло сообщение с дальней планеты Дельта-Континуум: в гостиницу собирались приехать все числа, расположенные между 0 и 1. Администратор гостиницы, разумеется, знала, что между 0 и 1 заключено «довольно много» чисел, например³√3/2, е 6 – π – π 5, 1/2, 3/156, е /47, (5 + 13√2)/213… Тем не менее она не предполагала, что расселение всех их вызовет какие-либо затруднения. Разве в гостинице уже не жило бесконечное количество бесконечных множеств? Что же может быть трудного в размещении всего одной-единственной бесконечной группы?

Но затруднения возникли, и все ее попытки их устранить не дали никакого результата. Ей ничего не оставалось, как снова обратиться за помощью к профессору Финкельштейну-Островскому-Канторовичу или Сигме и Лямбде. Омега решила позвонить профессору. К ее удивлению и разочарованию, заслуженный профессор не только не смог предложить решения, но и установил, что решения у этой задачи попросту нет .

– А если выселить из гостиницы все натуральные числа? Не поможет ли это? – все же не сдавалась Омега.

– Ничуть не поможет, – уверенно отвечал профессор.

– Как же может быть, что в бесконечной гостинице, тем более пустой, не хватит места для одной-единственной группы постояльцев? – по-прежнему не желала мириться с этой неприятной новостью Омега.

– Не упрямьтесь, – сказал профессор. – Вместо того чтобы искать способы расселения этих чисел, позвольте, я докажу вам, что в бесконечной гостинице не найдется места не только для всех чисел между 0 и 1, но даже и для всех чисел, записанных с использованием только цифр 0 и 1.

– Вы серьезно? – спросила администратор.

– Профессор Финкельштейн-Островский-Канторович всегда серьезен, когда говорит о математике или музыке, – ответил он, говоря о себе в третьем лице.

– Ну хорошо. Тогда извольте объясниться. – И Омега приготовилась выслушать его объяснение.

– Прежде всего мы должны договориться, что записываем все числа в бесконечной нотации. Я хочу сказать, что вместо 0,101 мы будем писать 0,101000… Теперь начнем с предположения, что нам все же удалось решить эту задачу, и мы смогли найти в гостинице номера для всех чисел.