Бенуа Мандельброт - Фрактальная геометрия природы

Зададим себе привычный вопрос. Как бы ни занимали математиков фигуры Серпинского, Менгера и им подобные, не очевидно ли, что для человека, изучающего Природу, степень ветвления не может представлять никакого интереса? Ответ так же привычен — для нас с вами! — как и вопрос. Степень ветвления обретает значимость уже в «реальном мире» конечных аппроксимаций, получаемых при остановке ведущей к фракталу интерполяции при некотором положительном конечном внутреннем пороге ε .

В самом деле, если дано приближение салфетки Серпинского, составленное из заполненных треугольников с длиной стороны ε , то можно разъединить область, линейный масштаб которой превышает ε , простым удалением трех или четырех точек, каждая из которых принадлежит границе между двумя соседними пустотами. Это число (3 или 4) не изменяется при улучшении приближения. Следовательно, с точки зрения ветвления, все приближения салфетки можно считать кривыми.

Все ковры, напротив, обладают общим свойством: никакая пара пустот не имеет общей границы. Для разъединения конечного приближения такой фигуры, при рассмотрении которой мы игнорируем пустоты, меньшие ε , необходимо удалять целые интервалы. И количество этих интервалов возрастает по мере того, как ε→0 . Уайберн [592] показал, что все фрактальные кривые, обладающие этим свойством, топологически идентичны (< гомеоморфны ►) и характеризуются тем, что никакая их часть не может быть отделена удалением одной точки.

С учетом предыдущих замечаний неудивительно, что конечность ветвления находит столь явные и четко очерченные области применения в тех случаях, когда фрактальная геометрия оказывается призвана подробно определить, в какой пропорции плоская фрактальная кривая сочетает в себе два своих стандартных предела: прямую и плоскость. Обобщая, можно сказать, что знать фрактальную размерность кривой отнюдь не достаточно. Например, при исследовании критических феноменов для моделей Изинга на фрактальной решетке авторами работы [165] было установлено, что наиболее важные результаты (< будь то при нулевой или при положительной температуре ►) непосредственно зависят от конечности величины R .

Вот и настало время дать объяснение, к которому мы ранее были не готовы. Причина, по которой магистраль кластера в критической бернуллиевой перколяции лучше моделируется салфеткой Серпинского, нежели ковром, проясняется следующим открытием Киркпатрика [265]. Даже в чрезвычайно больших решетках критическую магистраль можно разъединить удалением некоторого, по существу неизменного, малого количества связей (величины порядка 2). Даже принимая во внимание всевозможные отклонения, это открытие представляется мне весьма убедительным свидетельством того, что R<���∞ .

Существуют два варианта снежинки Коха, которые достигают ветвления без образования петель. Первый — плоская кривая, инициатором которой является квадрат, а генератор выглядит следующим образом:

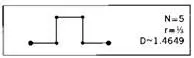
Как видно из рисунка, получаемая кривая ничуть не похожа на снежинку:

Другой пример — поверхность с нулевым объемом, бесконечной площадью и размерностью, равной ln6 / ln2 =2,58497 . Инициатором служит правильный тетраэдр. К средней четверти каждой грани (т. е. к треугольнику, вершинами которого являются середины ограничивающих грань ребер) приставляется другой тетраэдр, линейные размеры которого уменьшены в два раза. Процедура повторяется с каждой гранью получающегося в результате правильного (асимметричного и невыпуклого) 24-гранника, а затем снова и снова до бесконечности. Начиная со второго этапа построения, добавляемые тетраэдры касаются друг друга гранями без самопересечений. В конце концов они заполняют всю поверхность инициатора. Назовем каждую четверть этой конструкции, выросшую на одной из граней инициатора, пирамидой Коха.

Пирамида Коха воистину чудесна — если смотреть сверху, форма ее очень проста, однако в ней скрыто множество потаенных ходов и камер, потрясающих даже самое смелое воображение.

Если смотреть сверху, пирамида Коха — это тетраэдр, основанием которого служит равносторонний треугольник. Что касается трех остальных граней, то они представляют собой прямые равнобедренные треугольники, соединенные вершинами при прямых углах. Если приложить три пирамиды Коха к трем граням правильного тетраэдра, то получится простой куб.

А теперь поднимем нашу пирамиду вверх и стряхнем с нее песок пустыни. Рассматривая ее основание с некоторого расстояния, мы видим, что оно разделяется на четыре равных равносторонних треугольника. Однако на месте среднего треугольника находится отверстие, ведущее в «камеру первого порядка», которая имеет форму правильного тетраэдра, четвертая вершина которого совпадает с верхушкой пирамиды. Подойдя ближе и получив возможность разглядеть более мелкие детали, мы обнаруживаем, что и находящиеся в углах основания правильные треугольники, и верхние грани камеры первого порядка также не являются гладкими поверхностями. Их гладкость нарушается тетраэдральными камерами второго порядка. Аналогичным образом, при исследовании камер второго порядка, мы видим, что в середине каждой треугольной стены имеется треугольное же отверстие, ведущее в камеру третьего порядка. Чем глубже мы погружаемся в пирамиду, тем меньшие камеры открываются нашему взору, и конца им не видно.

Сумма объемов всех камер в точности равна объему всей пирамиды Коха. С другой стороны, если считать, что основания камер являются частью этих камер, а остальные три грани — нет, то окажется, что камеры не пересекаются ни в одной точке. Если бы строителям нашей пирамиды пришлось выдалбливать камеры в толще скалы, то им пришлось бы удалить всю породу, оставив лишь тонкую оболочку. Кривая, которой пирамида Коха опирается на плоскость, и «стены» камер представляют собой салфетки Серпинского.

Авторы работы [313] невольно сделали значительный вклад во фрактальную геометрию, попытавшись заполнить R E шарами, радиус каждого из которых имеет вид ρ k =ρ 0 r k , где r<1 ; число шаров радиуса ρ k на единицу объема имеет вид n k=n 0v k , где v — целое число вида v=(1−r)r −E , что накладывает жесткие ограничения на r . Таким образом, показатель распределения размеров пустот определяется следующим выражением: