Бенуа Мандельброт - Фрактальная геометрия природы

Перейдем к фрактальному аспекту. Размерность множества концов ветвей D , а размерность каждой ветви 1. Что касается целого, то оно, не будучи масштабно-инвариантным, все же характеризуется фрактальной размерностью, определяемой по формуле Хаусдорфа – Безиковича, причем эта размерность не может быть ни меньше D , ни меньше 1, а на деле оказывается равной большей из двух величин. Рассмотрим каждый из случаев отдельно.

Фрактальные деревья.Когда D>1 , фрактальная размерность всего дерева равна D . Несмотря на то, что ветви доминируют в конструкции как с точки зрения здравого смысла, так и топологически, во фрактальном смысле ими можно пренебречь. Так как D>D T , дерево представляет собой фрактальное множество, в котором величина D служит мерой ветвления. Таким образом, нам открывается еще одна грань фрактальной размерности в добавление к ее способности выступать качестве меры иррегулярности и фрагментации. Когда мы перейдем в главе 17 к не нитевидным деревьям, мы обнаружим, что гладкая поверхность с достаточным количеством острых локализованных «выступов» может оказаться чем-то «бóльшим», чем стандартная поверхность.

Субфрактальные деревья.В случае 0 линейная мера (совокупная длина) всего дерева конечна и положительна, так что его фрактальная размерность неизбежно равна 1. Следовательно, D=D T , т. е. такое дерево не является фрактальным.

Тем не менее, если подобрать единицы измерения таким образом, чтобы длина ствола составила 1−2r , то ветви (рассматриваемые как открытые интервалы) можно будет разместить вдоль пустот линейной канторовой пыли C , которая занимает интервал [0,1] и характеризуется теми же значениями N=2 и r , что и множество концов ветвей. Аналогичным образом, на множестве C можно разместить и сами концы ветвей. Получается, что интервал [0,1] целиком заполняется отображениями точек нашего дерева. Не отображаются только те точки, на которых держатся ветви. Эти точки образуют счетное остаточное множество.

Вспомним о замечании, сделанном нами по поводу чертовой лестницы на рис. 125 – ее форма необычна, но фракталом она не является. Если важность этих форм будет возрастать и далее, им может понадобиться особое и тщательно выбранное название. Пока же остановимся на субфракталах.

В качестве последнего эксперимента заменим прямолинейные ветви фрактальными кривыми с размерностью D * >1 . Когда D * , фрактальные свойства дерева определяются ветвями, а все дерево целиком представляет собой фрактал с размерностью D * . В случае же D>D * наше дерево будет фракталом с размерностью D .

Думаю, настала пора вводить новое определение. Фрактал F называется однородным, если все множества, полученные в результате пересечения F с диском или шаром, центр которого принадлежит F , имеют одинаковую топологическую (D T ) и фрактальную (D>D T ) размерности.

Очевидно, что кривые Коха, канторова пыль, разветвленные кривые и т. д. являются однородными фракталами. А остовы деревьев с D>0 из предыдущей главы следует отнести к фракталам неоднородным.

Вообще говоря, деревья могут считаться фракталами только отчасти: пересечение дерева и достаточно малого диска, центр которого принадлежит ветви, не является фракталом, но состоит из одного или нескольких интервалов.

До сих пор мы полагали, что деревья, изображенные на рис. 223, пусть едва-едва, но все же избегают самокасаний. На самом же деле, концы ветвей этих деревьев асимптотически касаются друг друга. В результате множество концов ветвей перестает быть пылью с D T =0 и становится кривой с D T =1 без малейшего изменения фрактальной размерности. Для описания этого нового класса фрактальных кривых я предлагаю термин расширенные фрактальные кроны. Заметим, что длина тени такой кроны возрастает с увеличением D .

Кривую, ограничивающую открытую область снаружи получающейся в результате фигуры, назовем просто «фрактальной кроной». Благодаря отсутствию «складок», присущих расширенной кроне, размерность этой кривой не дотягивает до D на величину, которая возрастает с увеличением D .

Поскольку для деревьев жизненно важен солнечный свет, ветви, заканчивающиеся в складках расширенной фрактальной кроны, скорее всего, засохнут. Садовник может либо позволить каким-то ветвям вырасти, а затем засохнуть из-за отсутствия света, либо составить более сложную программу, которая запретит расти именно этим ветвям. Я предпочел бы более простую программу.

Когда D<1 , слияние пыли с размерностью D в кривую невозможно. Если попытаться добиться самокасания посредством уменьшения угла θ между ветвями, то цель будет достигнута лишь тогда, когда угол станет равным 0 и дерево стянется в интервал. Если же пойти другим путем и зафиксировать длину тени дерева, а самокасания добиваться посредством вытягивания ветвей вверх, то цель не будет достигнута никогда: в пределе из дерева получится комбинация линейной канторовой пыли C и свисающих из каждой точки C полупрямых.

Многообразие фрактальных деревьев не сводится к тем формам, которые мы рассмотрели в предыдущих разделах. Вспомним, например, конструкцию, описанную на с. 202. А теперь возьмем в качестве кохова генератора крест, ветви которого имеют следующие длины: r в (верхняя), r н (нижняя), r б (боковые), причем выполняется равенство r В 2+r Н 2+2r б 2<1 . Каждая ветвь получившегося фрактального дерева, какой бы малой она ни была, в изобилии окружена подветвями. А если исключить корневую точку, то такие деревья масштабно-инвариантны без остатка.

Фейнман [149] пишет, что благодаря фрактальным деревьям он смог представить себе и смоделировать «струи», образующиеся при столкновениях частиц очень высоких энергий. Эту идею исследовал Дж. Венециано, о чем он сообщает в отчетах CERN.

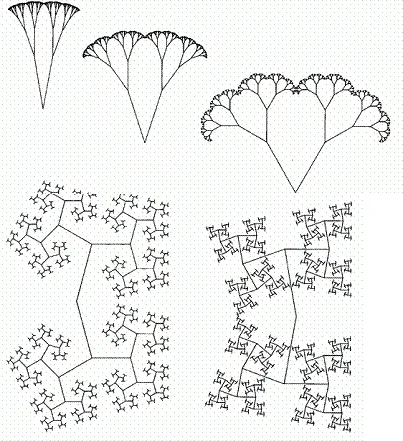
Рис. 223. Фрактальные зонтичные деревья и фрактальные кроны

Каждое дерево на этом рисунке имеет бесконечно тонкий ствол и неизменный угол θ между ветвями. Размерность D варьируется между 1 и 2, причем для каждого D угол θ принимает наименьшее возможное без самокасаний значение.