Бенуа Мандельброт - Фрактальная геометрия природы

Рис. 253. Самоинверсный фрактал (построение Мандельброта)

Верхняя фигура.В цепях Пуанкаре с M=4 по крайней мере один из дисков Δ ijk (назовем его Δ 123 ) всегда не ограничен и пересекается с диском Δ 341 . (На данном рисунке диск Δ 341 также не ограничен, однако в других случаях это не так.) Объединение дисков Δ 123 и Δ 341 (показанное на рисунке серым цветом) дает первое приближение области, внешней к кривой ℒ . Оно аналогично приближению области, внешней к кривой Коха K , с помощью правильного выпуклого шестиугольника (см. рис. 71).

Диски Δ 234 и Δ 412 также пересекаются, и их объединение (показанное на рисунке черным цветом) дает первое приближение внутренней области ℒ . Оно аналогично приближению внутренней области кривой K с помощью двух треугольников, образующих правильную шестиконечную звезду (см. рис. 71).

Средняя фигура. Второе приближение области, внешней к кривой ℒ , достигается добавлением к дискам Δ 123 и Δ 341 их инверсий относительно окружностей C 4 и C 2 , соответственно. Результат (серая область) аналогичен второму приближению области, внешней к кривой K , на рис. 71.

Соответствующее второе приближение внутренней области ℒ достигается добавлением к дискам Δ 234 и Δ 412 их инверсий относительно окружностей C 1 и C 3 , соответственно. Результат (черная область) аналогичен второму приближению внутренней области кривой K на рис. 71.

Нижняя фигура.Внешняя область ℒ (серый цвет) является объединением кланов Δ 123 и Δ 341 . Внутренняя же (черный цвет) – объединением кланов Δ 234 и Δ 412 . Тонкая структура внутренней области ℒ показана на рис. 255 внизу (при построении использованы разные цепи Пуанкаре). Черная и серая открытые области вместе покрывают всю плоскость (за вычетом кривой ℒ ).

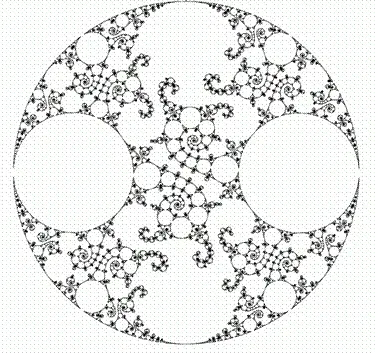
Рис. 254. Самографический фрактал (вблизи предела Пеано)

Группы, основанные на инверсиях, интересуют математиков, прежде всего потому, что они связаны с определенными группами гомографией. Гомография (называемая также гомографией Мебиуса или дробно-линейным преобразованием) отображает z - плоскость по закону z→(az+b)/(cz+d) , где ad−bc=1 . В наиболее общем виде эта гомография может быть представлена как результат инверсии, симметрии относительно линии (что есть вырожденная инверсия) и вращения. Вот почему при отсутствии вращения исследователь гомографией может почерпнуть много интересного из изучения групп, основанных на инверсиях. Очевидно, однако, что введение вращений открывает новые богатые возможности.

На рисунке изображен пример предельного множества ℒ для группы гомографий. Построил его Дэвид Мамфорд (в ходе исследований, стимулом для которых послужили новые результаты, о которых говорится в данной главе), а затем любезно разрешил опубликовать свое построение в этой книге. Фигура эта почти заполняет плоскость и демонстрирует поразительные аналоги (и равно поразительные различия) с почти заполняющей плоскость кривой, изображенной на рис. 270.

Фрактальная природа предельного множества группы гомографий в широком диапазоне условий была доказана Т. Акадзой, А. Ф. Бирдоном, Р. Боуэном, С. Дж. Паттерсоном и Д. Салливеном. См. [545].

Рис. 255. Знаменитый самоинверсный фрактал, исправленный вариант (построение Мандельброта)

Рисунок вверху слева воспроизводит рис. 156 из книги Фрикке и Клейна [154], который призван изображать самоинверсный (в моей терминологии) фрактал, генератор которого состоит из пяти окружностей, ограничивающих центральную область (она показана черным цветом). Этот рисунок весьма часто появляется в математической литературе.

Действительной формой этого фрактала является контур фигуры, изображенной вверху справа; фигура эта построена с помощью моего метода оскулирующих σ - дисков. Расхождение, конечно, ужасное. Фрикке знал, что кривая ℒ должна содержать окружности, и велел иллюстратору включить их в рисунок. Обо всем остальном он не знал и, очевидно, даже не подозревал, насколько иррегулярной фигуры ему следует ожидать.

В действительности кривая ℒ включает в себя границу ℒ * фигуры, построенной справа внизу с использованием моего алгоритма. Эта граница ℒ * представляет собой самоинверсный фрактал, соответствующий четырем из тех порождающих окружностей, что образуют цепь Пуанкаре. Ясно видно, что преобразования ℒ * при иных инверсиях принадлежит ℒ . Этот рисунок подробно рассмотрен в работе [400].

В этой главе мы рассмотрим два семейства очень простых нелинейных преобразований (или отображений) и исследуем несколько таких фрактальных множеств, которые при этих преобразованиях остаются инвариантными и для которых они могут служить генераторами.

Во-первых, дробно-линейное преобразование вещественной линии поможет нам лучше понять нашу старую знакомую – канторову пыль. Эти замечания, конечно, можно было вставить в главу 8, однако мне кажется, что они будут лучше восприняты на данном этапе.

Они, в частности, помогают оценить результаты вещественных и комплексных квадратичных преобразований вида x→f * (x)=x 2 −μ , где x и μ вещественны, и z→f * (z)=z 2 −μ , где z=x+iy и μ - комплексные числа.

Элементарный случай μ=0 довольно скучен с геометрической точки зрения, однако другие значения μ ведут к потрясающим фрактальным красотам, многие из которых были впервые продемонстрированы в статье [398].

Удобнее всего получать упомянутые инвариантные формы с помощью итераций (т. е. многократных применений) одного из вышеуказанных преобразований. Исходные значения мы будем обозначать через x 0 или z 0 , а результаты k - й итерации функции f * - через x k или z k .

Хронологически изучение итераций можно разделить на три этапа. Первый, связанный с комплексной переменной z , прошел под знаменами Пьера Фату (1878 – 1929) и Гастона Жюлиа (1893 – 1978). Их публикации являются шедеврами классического комплексного анализа, ими восхищаются математики, однако на их фундаменте чрезвычайно сложно что-нибудь построить. В своей работе, о которой данная глава дает лишь весьма сжатое представление, я стараюсь придать бóльшую наглядность их основным открытиям, объединяя анализ с физикой и подробными иллюстрациями, в результате чего обнаруживается великое множество неизвестных ранее фактов.