Бенуа Мандельброт - Фрактальная геометрия природы

Вообще говоря, в примерах, стимулировавших это обобщение, последовательность g(t) либо действительно случайна, либо ведет себя так, словно является случайной. К рассмотрению случайности мы с вами приступим только в следующей главе, однако я не думаю, что это обстоятельство может нам помешать. Гораздо серьезнее другое: динамические системы представляет собой воплощенный образчик полностью детерминированного поведения, и поэтому просто не вправе допускать какую бы то ни было случайность! Мы, однако, можем ввести воздействие случайности, не постулируя ее явно – нам нужно лишь присвоить функции g(t) значение какого-нибудь в достаточной степени перемешивающего эргодического процесса. Возьмем, например, иррациональное число β и сопоставим функции g(t) целую часть числа σ f(t)=β tσ f(0) . Здесь стоило бы сделать еще несколько заявлений, принципиально не сложных, но весьма громоздких, так что я, пожалуй, от этого воздержусь.

Сторонники «странных» аттракторов выдвигают в свою защиту следующие два соображения. А) . Поскольку динамические системы со стандартными аттракторами не в состоянии объяснить турбулентность, то, может быть, ее удастся объяснить с помощью систем с аттракторами, топологически более «странными». (это напоминает мое собственное рассуждение (см. главу 11) – высказанное, кстати, совершенно независимо от приведенного – о том, что если дифференциальное уравнение не имеет стандартных особенностей, следует попытать счастья с особенностями фрактальными. Б) . Аттракторы до смешного простых систем – таких, как z→λz(1−z) при вещественных λ и z в интервале [0,1] - действительно странны и во многих отношениях характерны для более сложных и более реалистичных систем. Таким образом, топологически странные аттракторы, вне всяких сомнений, являются, скорее, правилом, нежели исключением.

Все известные «странные» аттракторы представляют собой фрактальные множества.Для многих «странных» аттракторов существуют оценки размерности D . Во всех случаях D>D T . Следовательно, эти аттракторы суть не что иное, как фрактальные множества. Во многих случаях размерность D «странно – аттракторных» фракталов служит мерой не иррегулярности, а того, как накладываются друг на друга гладкие кривые или поверхности – своего рода фрагментации (см. главу 13).

С. Смейл представлял свой знаменитый аттрактор, называемый соленоидом, дважды. Оригинальное определение было чисто топологическим (размерность D при этом оставалась неопределенной), пересмотренный же вариант имеет метрический характер (см. [527], с. 57). Я, в свою очередь, предложил ввести в теорию странных аттракторов понятие размерности D и оценил в [392] значение D для этого пересмотренного варианта. Значение D=2,06 для аттрактора Зальцмана – Лоренца ( v=40 , σ=16 и b=4 ) было получено независимо от меня Я. Г. Синаем и М. Г. Веларде (источник – частная беседа). Это значение больше 2, но не намного, т.е. этот аттрактор определенно не является стандартной поверхностью, но близок к таковой. Мори и Фудзисака [437] подтверждают мое значение D для аттрактора Смейла и значение D для аттрактора Зальцмана – Лоренца. Они также нашли размерность D отображения Энона (a=1,4;b=0,3) , которая оказалась равной 1,26. Ожидается появление многих других статей в том же духе.

Обратное утверждение.Являются ли все фрактальные аттракторы странными – вопрос семантики. Все больше авторов согласны со мной в том, что аттрактор, как правило, можно считать странным, если он фрактален. Мне такое отношение представляется вполне здравым, если учесть, что слово «странный» выступает как синоним слов «чудовищный», «патологический» и других подобных эпитетов, которыми некогда награждали отдельные фрактальные множества.

Однако прилагательному «странный» иногда придается некий особый терминологический смысл настолько, надо сказать, особый, что аттрактор Зальцмана – Лоренца характеризуется не просто как «странный», но как «странно – странный». В этом свете «странность» аттрактора связывается главным образом с нестандартными топологическими свойствами, в то время как нестандартные фрактальные свойства просто сопутствуют им в качестве «нагрузки». Замкнутая кривая с двойными точками не является в этом смысле «странной», какой бы смятой она ни была: это значит, что большинство из исследованных мною фрактальных аттракторов нельзя считать странными.

При таком определении термина «странный» рассуждения в предыдущем разделе теряют всякую привлекательность. Однако если модифицировать понятие странности с тем, чтобы оно из топологического стало фрактальным, то эту привлекательность можно вернуть. Вот почему я считаю, что победы в споре достойны те, кто определяет «странное» как «фрактальное». А поскольку они и в самом деле побеждают, я не вижу большого смысла в сохранении термина, необходимость в котором исчезла в тот момент, когда я показал, что фракталы не более странны, чем, скажем, горы или береговые линии. Кроме того, не стану скрывать: к термину «странный» я испытываю какую-то личную неприязнь.

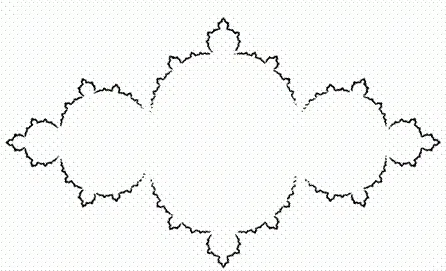
Рис. 282 и 283. Притяжение к фракталам

Приведенные здесь фигуры иллюстрируют длинные орбиты последовательных состояний двух разложимых динамических систем. Нагрудник фараона на рис. 283 представляет собой самоинверсное (см. главу 18) множество, основанное на четырех инверсиях, подобранных таким образом, чтобы предельное множество ℒ являлось совокупностью окружностей. Дракон Сан-Марко на рис. 282 – самоквадрируемое (см. главу 19) множество и основан на двух инверсиях отображения x→3x(1−x) .

Определяющий индекс в этих случаях выбирается из четырех (или, соответственно, двух) возможностей с помощью псевдослучайного алгоритма, примененного 64 000 раз. Несколько первых точек на рисунке опущены.

Области в окрестностях точек заострения и самопересечения заполняются чрезвычайно медленно.

Хотя фундаментальные разделы фрактальной геометрии имеют дело исключительно с детерминированными конструкциями, истинный смысл и практическая значимость этих разделов остается неочевидной до тех пор, пока мы не исследуем случайные фракталы. И наоборот, изучение фракталов углубляет понимание природы случайности – по крайней мере, мне так кажется.