Эдвард Шейнерман - Путеводитель для влюбленных в математику

Мы столкнулись с противоречием. С нами уже такое случалось. В главе 1 мы вообразили число N , которое, как выяснилось, (a) делится на некое простое число и (b) не делится ни на какое простое число. Разумеется, это невозможно. Если мы пришли к противоречию, значит, мы исходили из ложной посылки. Так оно и было: мы предположили, что количество простых чисел конечно, и пришли к двум прямо противоположным выводам. Если вывод абсурден, то изначальное предположение было ошибочным. Неверно, что простые числа можно пересчитать: это приводит к бессмыслице. Таким образом, простых чисел бесконечно много.

Что касается парадокса Ньюкома, мы сделали два неявных допущения.

Первое допущение – относительно Игрока. Может ли он сделать независимый выбор? Обладают ли человеческие существа свободной волей? Разумеется, нельзя (и мы даже не будем пытаться) в точности разрешить эту старую как мир философскую проблему [233] Просто для справки: конечно же, вы обладаете свободой воли. Я не знаю, как вам могло прийти в голову, что это не так! .

Второе – относительно Предсказателя. Действительно ли он способен предвидеть поступки другого человека? Ясно, что в целом поведение людей может быть предсказано с большой долей уверенности. Но в нашей игре Предсказатель пытается предугадать выбор одного-единственного индивидуума, а ведь это весьма зыбкая материя. Точность 95 % неправдоподобно высока.

Однако вот что интересно: противоречие не исчезает, даже если Предсказатель прав в 51 % случаев! Аргумент «не оставляйте деньги на столе» по-прежнему не работает. Вот расчет среднего выигрыша:

• Если вы берете только ящик № 2, средний выигрыш составляет 1 000 000 × 0,51 + 0 × 0,49 = 510 000 долларов.

• Если вы берете оба ящика, средний выигрыш составляет 1 000 × 0,51 + 1 001 000 × 0,49 = $491 000 долларов.

Даже если Предсказатель предугадывает ваше решение с точностью 51 %, вам лучше выбрать только ящик № 2! Разница в средних выигрышах на сей раз невелика, поэтому расчеты не вызывают особых эмоций, но выигрышная стратегия остается прежней [234] А теперь головоломка: найдите уровень точности предсказаний, при котором обе стратегии дают одинаковый средний выигрыш, и противоречие исчезает. Ответ – в конце главы. .

Итак, вот два допущения, приводящих к парадоксу:

– Игрок обладает свободой воли;

– Предсказатель предугадывает решение Игрока с высокой точностью.

Иными словами, свобода выбора и уверенное предсказание будущего несовместимы.

Вообразим, что в роли Игрока – компьютерная программа, а в роли Предсказателя – мы, человеческие существа. По правилам, Игроку запрещено играть в орлянку; таким образом, компьютер не должен совершать случайного выбора [235] На самом деле большинство компьютеров содержит генератор псевдослучайных чисел. Компьютерная программа генерирует случайные величины, но, разумеется, следует четкому алгоритму. В главе 21 рассказано, как детерминированные процессы могут приводить к непредсказуемым результатам. .

У компьютера есть все те же две возможности: выбрать оба ящика или только ящик № 2. Как он поступит?

Мы можем с легкостью предсказать выбор компьютера. Нам нужно всего лишь сделать копию компьютерной программы, запустить на другом компьютере и следить за ее действиями. Наше предсказание будет идеальным (если компьютер не заглючит). Когда игра начнется, мы убедимся в безошибочности предсказания. Практически без исключений выбор двух ящиков принесет компьютеру тысячу долларов, а выбор ящика № 2 принесет миллион долларов.

Если нас попросят разработать программу для парадокса Ньюкома, наше решение будет кристально ясно. Вот вся программа:

print («Я беру только ящик № 2»)

Мы запускаем программу, компьютер каждый раз получает миллион долларов, и мы счастливы.

Нет никакого резона выбирать оба ящика. Действия компьютера полностью предсказуемы (потому что мы имеем дело с машиной, а не с человеком), и выбор двух ящиков всякий раз будет приносить всего лишь 1000 долларов.

Почему противоречие возникает, когда в роли Игрока оказывается человек, и пропадает, когда в роли Игрока выступает компьютер? Парадокс Ньюкома подразумевает свободу воли: никакой Предсказатель не в силах в точности предвидеть наши действия.

На русском языке

1. Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике . – М.: Мир, 1965.

2. Харди Г. Г. Апология математика. – Ижевск: НИЦ «Регулярная и хаотическая динамика», 2000.

На английском языке

1. Peter Beckmann. A History of π . St. Martin’s Press, third edition, 1976.

Edward B. Burger and Michael Starbird. The Heart of Mathematics: An Invitation to Effective Thinking . Wiley, third edition, 2009.

2. Underwood Dudley. A Budget of Trisections . Springer, 1987.

3. Richard P. Feynman, Robert B. Leighton, and Matthew Sands. The Feynman Lectures on Physics . Addison-Wesley Publishing Company, 1963.

4. Martin Gardner. Free will revisited, with a mind-bending prediction paradox Newcomb . Scientific American, 229, July 1973.

5. G. H. Hardy. Mathematician’s Apology . Cambridge University Press, 1940

6. H. E. Huntley. The Divine Proportion . Dover, 1970.

7. Nicholas D. Kazarinoff. Ruler and the Round: Classic Problems in Geometric Constructions . Dover, third edition, 2003.

8. Mario Livio. The Golden Ratio: The Story of PHI, the World’s Most Astonishing Number . Broadway, 2003.

9. Paul Lockhart. A Mathematician’s Lament: How School Cheats Us Out of Our Most Fascinating and Imaginative Art Form . Bellevue Literary Press, 2009.

10. Eli Maor. e: The Story of a Number . Princeton University Press, 2009.

11. Paul J. Nahin. An Imaginary Tale: The Story of 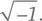Princeton University Press, 2010.

12. James R. Newman. The World of Mathematics . Simon & Schuster, 1956. This four-volume collection is also available from Dover.

13. Mark Nigrini. Benford’s Law: Applications for Forensic Accounting, Auditing, and Fraud Detection . Wiley, 2012.

14. E. Arthur Robinson and Daniel H. Ullman. A Mathematical Look at Politics . CRC Press, 2010.

15. Edward R. Scheinerman. Mathematics: A Discrete Introduction . Brooks/Cole, third edition, 2012.

16. Eric W. Weisstein. Mathworld – a Wolfram web resource, http://mathworld.wolfram.com/.

На французском языке

M. L. Wantzel. Recherches sur les moyens de reconnaître si un Problème de Géométrie peut se résoudre avec la règle et le compass . Journal de Mathématiques Pures et Appliquées., 1 (2): 366–372, 1837.

Кто-то сочтет, что слова «радость» и «красота» неприменимы к математике, но не стоит путать чудесную математику со скучной арифметикой. Мы же не ставим знак равенства между чтением великой литературы и зазубриванием правил орфографии. – Здесь и далее, кроме особенно оговоренных случаев, примечания автора.

Доказательство того, что простых чисел бесконечно много, вы обнаружите в главе 1.

Годфри Харди (1877–1947) – профессор Оксфордского и Кембриджского университетов, известный своими работами по теории чисел и математическому анализу. – Прим. пер.