Эдвард Шейнерман - Путеводитель для влюбленных в математику
- Название:Путеводитель для влюбленных в математику
- Автор:
- Жанр:
- Издательство:Литагент Альпина
- Год:2018
- Город:Москва
- ISBN:978-5-9167-1131-8
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Эдвард Шейнерман - Путеводитель для влюбленных в математику краткое содержание
Путеводитель для влюбленных в математику - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
33
В англоязычных странах в качестве разделителя разрядов используется запятая, в России – неразрывный пробел, который ставится только в числах с пятью и более разрядами. – Прим. ред.
34
Чтобы отличить запись в двоичной системе от записи в десятичной, мы будем ставить нижний индекс: 1101 2или 1101 10.
35
В английской традиции записи целую часть десятичного числа от дробной отделяет точка, в русской – запятая. – Прим. ред.
36
В случае с двоичной системой неправильно говорить «десятичная запятая», лучше называть ее двоичной запятой, или запятой в позиционном представлении числа.
37
Программисты нередко пользуются шестнадцатеричной системой счисления. В десятичной системе 10 цифр (от 0 до 9), в шестнадцатеричной нам нужно 16 разных символов, поэтому числа от 10 до 15 обозначают с помощью букв от A до F.
38
До бесконечности (лат.). – Прим. пер.
39
Строго говоря, это утверждение тоже надо доказать. – Прим. науч. ред.
40
Проверьте, насколько хорошо вы усвоили материал, и выразите 0,123123123123… в виде обыкновенной дроби. Ответ в конце главы.
41
Так как делить на ноль нельзя, я имею в виду такие операции, как 7/5.
42
Термин «рациональные числа» происходит от латинского слова ratio, но вовсе не потому, что они, в отличие от прочих, обладают здравым смыслом.
43
Не со всеми: есть физические величины, про которые нет оснований полагать, что отношения между ними выражаются в рациональных числах. Впрочем, как следует из сказанного выше, можно добиться сколь угодно точного приближения рациональными числами. – Прим. науч. ред.
44
Здесь мы рассматриваем исключительно квадратные корни из неотрицательных чисел. В главе 5 мы увидим, что в математике есть область, где можно извлекать квадратный корень из отрицательного числа.
45
Задача о бисекции угла существенно проще. Нет ничего сложного в том, чтобы с помощью циркуля и линейки прочертить луч, разделяющий заданный угол на два равных между собой угла.
46
Пьер Ванцель строго доказал, что задачи об удвоении куба и трисекции угла неразрешимы, в 1837 году.
47
Неразрешимость задачи о квадратуре круга стала ясна в 1882 году, когда Фердинанд фон Линдеман доказал, что число π трансцендентно. – Прим. пер.
48
Пифагор Самосский (VI–V вв. до н. э.) – древнегреческий философ, математик, мистик, основатель религиозного движения пифагорейцев. – Прим. пер.
49
Число 9/8 над стрелкой означает, что частота ноты справа в 9/8 раза больше частоты ноты слева.
50
Подобран венецианскими композиторами и теоретиками музыки в XVI веке. – Прим. пер.
51
Равномерно темперированный строй господствует в европейской музыке с XVIII века, однако его теоретическое обоснование встречается уже в работах XVI века, причем не только в Европе, но и в Китае. – Прим. пер.
52
Доказательство похоже на доказательство того, что значение √2 иррационально. Попробуйте найти его самостоятельно.
53
Мужские вокальные ансамбли в США, исполняющие популярную музыку а капелла. – Прим. пер.
54
Множество всех действительных чисел обозначают ℝ.
55
См. главу 3, где подробнее рассказано о периодических десятичных дробях.
56
Символ i для обозначения мнимой единицы предложил в конце X VIII века Леонард Эйлер, взяв первую букву латинского слова imaginarius – «мнимый». – Прим. пер.
57
На самом деле так называемые действительные числа ничуть не более реальны, чем мнимые. Мы не кладем в чашку кофе минус три кубика сахара и никогда не говорим, что расстояние от пункта A до пункта B равно в точности √2 Действительные числа полезны для измерения таких физических явлений, как температура или площадь. Мнимые числа полезны в других областях физики, включая квантовую механику и электронику. Все числа мнимые в том плане, что созданы нашим сознанием.
58
Строго говоря, в системе действительных чисел должны выполняться соотношения порядка, аксиомы сложения и умножения и свойство полноты. Однако все эти выкладки, конечно, слишком сложны для научно-популярного обзора. – Прим. пер.
59
Вот вам испытание: найдите все кубические корни из i .
60
То есть уравнение вида c 0+ c 1 x 1+ … + c mx m = 0. – Прим. пер.
61
На языке математики поле – это такое множество, для элементов которого заданы операции сложения и умножения, обладающие набором определенных свойств (так называемые аксиомы поля). Через них можно определить вычитание и деление. Все эти операции не должны выводить за границы данного множества. – Прим. пер.
62
«π» – триллер 1998 года, режиссер Даррен Аронофски. Главный герой фильма занимается теорией чисел. – Прим. пер.
63
Имеется в виду одеколон Pi Givenchy. – Прим. пер.
64
День π отмечают 14 марта (3.14), потому что π ≈ 3,14.
65
Дробь 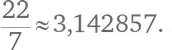 Другое соотношение ближе к истине:
Другое соотношение ближе к истине: 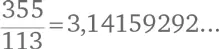
66
Если повезет, вы найдете их в магазине настольных игр. Правильный 20-гранник называется икосаэдр . См. главу 16.
67
На самом деле достаточно перебрать N ( N –1) / 2 вариантов, потому что у пар ( k, l ) и ( l, k ), очевидно, будут одинаковые общие делители; ясно также, что число не может быть взаимно простым само с собой. Поэтому достаточно заполнить не весь квадрат, а треугольник выше главной диагонали. – Прим. науч. ред.
68
Леонард Эйлер (1707–1783) – математик, механик, астроном. Работал в Швейцарии, Пруссии и России. Также изучил медицину, химию, ботанику, воздухоплавание, теорию музыки, множество европейских и древних языков. – Прим. пер.
69
Эйлер не называл это число своим именем, но именно он выбрал для него букву е . Подтолкнула ли его к этому гордыня – до сих пор предмет спора историков науки. Как бы то ни было, Эйлер было довольно скромным человеком.
70
Увы, все формулы для е весьма сложны. Это не просто иррациональное число, как √2 (см. главу 4), но и трансцендентное, как π (см. главу 6).
Читать дальшеИнтервал:
Закладка:










