Эдвард Шейнерман - Путеводитель для влюбленных в математику
- Название:Путеводитель для влюбленных в математику
- Автор:
- Жанр:
- Издательство:Литагент Альпина
- Год:2018
- Город:Москва
- ISBN:978-5-9167-1131-8
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Эдвард Шейнерман - Путеводитель для влюбленных в математику краткое содержание
Путеводитель для влюбленных в математику - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
71
Разница в 1 цент объясняется тем, что в первом случае мы каждый раз округляли прибыль до сотых.
72
В первый месяц банк выплатит нам 0,8333 % процента от первоначальной суммы, то есть 8,33 %. Теперь у нас в общей сложности $1008,33.
73
На самом деле длительность года чуть больше 365 дней, но мы упростим расчеты.
74
Экспоненциальная убыль встречается в природе. Пример – радиоактивный распад атомов.
75
Восклицательный знак означает факториал. Подробнее о факториале вы можете прочесть в главе 10.
76
Примечание для тех, кто знаком с логарифмами: для того чтобы выяснить, насколько редко встречаются простые числа, когда мы рассматриваем большие величины, можно посчитать количество простых чисел между 1 и каким-нибудь крупным числом N . Важнейший результат в теории чисел показывает, что чем больше N , тем ближе количество простых чисел между 1 и N к величине 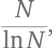 где ln N – логарифм числа N по основанию e , или натуральный логарифм N . Этот результат зафиксирован в так называемой теореме о распределении простых чисел.
где ln N – логарифм числа N по основанию e , или натуральный логарифм N . Этот результат зафиксирован в так называемой теореме о распределении простых чисел.
77
Числитель в этом выражении – пример телескопического ряда, где все слагаемые взаимно уничтожаются. Представьте себе складной телескоп, состоящий из нескольких частей. Точно так же слагаемые телескопического ряда вкладываются друг в друга.
78
Я здесь пропускаю множество этапов вывода формулы Эйлера. Я хочу просто объяснить, что значит возводить число в мнимую степень, и дать общую картину доказательства. В полном виде оно включает тригонометрические выкладки и такие сложные вычисления, которым не место в этой книге.
79
Георг Кантор (1845–1918) – немецкий математик, создатель теории множеств. Последние годы провел в психиатрической лечебнице. – Прим. пер.
80
Работы Кантора подвергались нещадной критике как со стороны математиков, так и со стороны философов и теологов. Но спустя некоторое время он добился признания как первооткрыватель новой области математики.
81
Обычно множество обозначают с помощью фигурных скобок.
82
Математики называют взаимно однозначное соответствие биекцией.
83
Нам не обязательно знать все элементы |A| или |B|, чтобы констатировать, что |A| = |B|.
84
Это множество натуральных чисел, его обычно обозначают ℕ. – Прим. науч. ред.
85
Вот две задачки. Какое число будет стоять справа на сотой строке перечня? Какое число слева будет соответствовать числам 100 и –100 справа? Ответ – в конце главы.
86
При первом чтении главы эти два абзаца можно пропустить. Мы уточняем одну техническую деталь, чтобы сделать аргументацию полной и неуязвимой.
87
Символ א обозначает первую букву древнееврейского алфавита: алеф. Символ 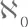 читают «алеф нуль».
читают «алеф нуль».
88
Вообще говоря, из сказанного это не следует; существование таких чисел надо специально доказывать. – Прим. науч. ред.
89
Этот подход, известный как наивная теория множеств, использовал Кантор и другие математики.
90
Может ли одно множество быть элементом другого? Разумеется! Скажем, множество {1, 2} входит во множество {0, {1, 2}, 3, 6, 7}. В этом множестве пять элементов: числа 0, 3, 6, 7 и множество {1, 2}.
91
Одно из многочисленных достижений Рассела – Нобелевская премия по литературе за 1950 год.
92
Этот парадокс называют антиномией Рассела.
93
Этот подход известен под названием «аксиоматическая теория множеств». Общепринятые правила поведения и формирования множеств названы в честь своих создателей, Эрнста Цермело (Ernst Zermelo) и Абрахама Френкеля (Abraham Fraenkel): ZF-аксиомы.
94
Если хоть одно такое множество существует, |ℝ|> алеф_1 . – Прим. науч. ред.
95
Эта глава повествует о знаменитых числах Фибоначчи: 1, 1, 2, 3, 5, 8, 13, 21 и т. д. Этот ряд был назван в честь Леонардо Пизанского, больше известного как Фибоначчи. (Леонардо Пизанский (1170–1250) – один из первых крупных математиков средневековой Европы. Прозвище Фибоначчи означает «сын Боначчи». Автор «Книги абака», излагающей десятичную систему счисления. – Прим. пер. )
96
В задаче о квадратах и домино мы выяснили: F 1= 1, а F 2= 2. Но числа Фибоначчи начинаются с F 0= 1. Как это согласуется с условиями задачи? Сколько существует способов заполнить на тех же условиях рамку 0 × 1? Длина квадрата и длина костяшки домино, как ни крути, больше нуля, потому есть искушение сказать, что ответ равен нулю, но это не так. Прямоугольник 0 × 1 уже заполнен, там нет щелей; нам не понадобится ни квадрат, ни костяшка домино. Таким образом, есть всего один способ действия: не брать ни квадрата, ни костяшки домино. Понимаете? В таком случае я вас поздравляю. У вас душа математика!
97
Слово «комбинаторный» образовано от существительного «комбинаторика» – названия раздела математики, предметом которого является подсчет вариантов в задачах, схожих с облицовкой прямоугольника. Слово «комбинаторика», в свою очередь, образовано от слова «комбинации».
98
Популярная в США телевикторина. Аналоги Jeopardy! выходят в разных странах; в России это – «Своя игра». – Прим. ред.
99
Число k может принимать значения от 1 до n + 1, но не больше, потому что иначе последняя костяшка домино высунется за пределы рамки.
100
Жак Бинe (1786–1856) – французский математик, механик и астроном. Формула для чисел Фибоначчи названа в честь Бине, хотя почти на сто лет раньше ее вывел Абрахам де Муавр (1667–1754). – Прим. пер.
101
Для читателей, не понаслышке знакомых с интегралами, приведу еще одну эстетически безупречную формулу: 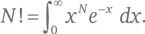 Она не слишком хороша для вычислений, но дьявольским образом позволяет находить факториал дробных чисел. Например, в соответствии с приведенной выше формулой
Она не слишком хороша для вычислений, но дьявольским образом позволяет находить факториал дробных чисел. Например, в соответствии с приведенной выше формулой 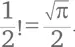
102
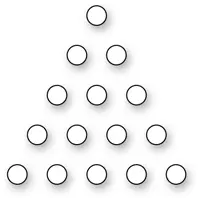
Такие числа называют треугольными, потому что они равны сумме объектов, расположенных в форме треугольника:
103
Интервал:
Закладка:










