Эдвард Шейнерман - Путеводитель для влюбленных в математику
- Название:Путеводитель для влюбленных в математику
- Автор:
- Жанр:
- Издательство:Литагент Альпина
- Год:2018
- Город:Москва
- ISBN:978-5-9167-1131-8
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Эдвард Шейнерман - Путеводитель для влюбленных в математику краткое содержание
Путеводитель для влюбленных в математику - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
144
Георг Пик (1859–1942) – австрийский математик, профессор Университета Карла-Фердинанда в Праге. – Прим. пер.
145
Как ни странно, некоторые из четырех центров могут лежать вне треугольника! Догадываетесь почему? Ответ – в конце главы.
146
Фрэнк Морли (1860–1937) – заведующий кафедрой в Университете Джонса Хопкинса в Балтиморе, главный редактор American Journal of Mathematics. Он доказал эту теорему в 1899 году, когда изучал свойства кривых, заданных кубическим уравнением. – Прим. пер.
147
Равнобедренным называют такой треугольник, где две стороны равны между собой.
148
Из теоремы Пифагора следует, что диагональ квадрата со стороной 1 равна √2. Дело в том, что диагональ квадрата рассекает его на два прямоугольных треугольника; длина их катетов равна 1, в то время как длина гипотенузы равна некоторой величине c . По теореме Пифагора c ² = 1² + 1² = 2. Извлечение квадратного корня дает 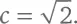 Об этом числе шла речь в главе 4.
Об этом числе шла речь в главе 4.
149
Это доказательство было найдено Бхаскарой, индийским математиком X II века.
150
Джеймс Гарфилд (1831–1881) был самоучкой, преподавал в школах и вузе, занимался адвокатурой. Воевал на стороне северян, был видным деятелем Республиканской партии. Погиб от руки террориста через три месяца после вступления в должность президента. – Прим. пер.
151
Трапеция – это четырехугольник, в котором две стороны параллельны друг другу, а две другие – нет. Параллельные стороны называют основаниями трапеции. Площадь трапеции можно вычислить по формуле 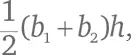 где b 1и b 2 – длины оснований, а h – расстояние между ними. Обратите внимание, что трапеция в доказательстве Гарфилда – половина фигуры, разобранной в нашем первом доказательстве, образованная путем рассечения малого квадрата по диагонали.
где b 1и b 2 – длины оснований, а h – расстояние между ними. Обратите внимание, что трапеция в доказательстве Гарфилда – половина фигуры, разобранной в нашем первом доказательстве, образованная путем рассечения малого квадрата по диагонали.
152
Мы обсуждали комплексные числа в главе 5.
153
В русскоязычной литературе обычно используют термин «модуль». – Прим. пер.
154
Головоломка!Числа 1, –1, i и – i имеют абсолютную величину 1, но это не единственные в своем роде числа. Опишите геометрическим способом все комплексные числа с абсолютной величиной 1. Ответ – в конце главы.
155
Прямоугольный треугольник со сторонами 3, 4 и 5 был известен уже древним египтянам.
156
Если хотите, можете пока просто поверить мне на слово, что | z ²| = | z |² для всех комплексных чисел. Вскоре вы увидите, как это доказать с помощью несложных алгебраических выкладок.
157
Комплексное число z = x + yi , где x и y – целые числа, называют гауссовым целым числом.
158
Эта история – священный миф математического сообщества, она пересказана во множестве книг и статей. Действительно ли Ферма нашел доказательство? Сомнительно. Более интересный вопрос: Ферма верил, что нашел доказательство, или разыгрывал читателей? Я предпочитаю второй вариант.
159
Сэр Эндрю Джон Уайлс (род. 1953) – британский и американский математик, профессор Оксфордского университета. – Прим. пер.
160
Математики различают окружность (линию) и круг (участок плоскости, ограниченный окружностью). (Точно так же различаются сфера (поверхность) и шар (область пространства, ограниченная сферой). – Прим. науч. ред. )
161
Теперь мы заполняем не поднос консервными банками, а большую коробку шарами одного радиуса. Пример наиболее плотной упаковки вы обнаружите в ближайшем супермаркете в отделе с фруктами, если увидите пирамиду апельсинов.
162
Точное соотношение равно 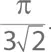
163
Томас Хэйлс (род. 1958) – профессор Питтсбургского университета. – Прим. пер.
164
Рене Декарт (1596–1650) – французский философ, математик, физик и физиолог, создатель аналитической геометрии и современной алгебраической символики. – Прим. пер.
165
Соответственно, когда кривизна стремится к бесконечности, окружность схлопывается в точку. – Прим. пер.
166
Фредерик Содди (1877–1956) – английский радиохимик, лауреат Нобелевской премии 1921 года «за вклад в химию радиоактивных веществ и за исследование происхождения и природы изотопов». – Прим. пер.
167
Блез Паскаль (1623–1662) – французский математик, физик и философ. – Прим. пер.
168
В общем виде теорема Паскаля формулируется так: если шестиугольник (выпуклый или самопересекающийся) вписан в окружность или любое другое коническое сечение (эллипс, параболу, гиперболу), точки пересечения трех пар противоположных сторон лежат на одной прямой. – Прим. пер.
169
Высота равностороннего треугольника со стороной 2 рассекает его на два прямоугольных треугольника с гипотенузой длиной 2 и катетом длиной 1. По теореме Пифагора мы можем вычислить длину оставшегося катета.
170
Стороны правильного семиугольника имеют равную длину, и углы также равны между собой.
Головоломка.Углы правильного семиугольника равны между собой. Но чему они равны? Подсказка: помните, что сумма углов треугольника равна 180°. Ответ – в конце главы.
171
Отрезки одинаковой длины или углы одинаковой величины называют конгруэнтными. Две фигуры конгруэнтны, если они совпадают при наложении друг на друга.
172
Древнегреческий философ Платон не был первооткрывателем этих пространственных фигур, однако подробно описал их в трактате «Тимей» (около 360 года до н. э.), где сказано, что образцом Вселенной для Демиурга послужил додекаэдр, стихия огня состоит из массы мельчайших тетраэдров, стихия земли – из кубов, стихия воздуха – из октаэдров, стихия воды – из икосаэдров. – Прим. пер.
173
Если вы сосредоточенно изучите таблицу в поисках взаимосвязей, то заметите, что параметры для куба и октаэдра симметричны: (8, 12, 6) и (6, 12, 8). Так же обстоит дело с додекаэдром и икосаэдром: (20, 30, 12) и (12, 30, 20). Эту перекличку называют дуальность.
Если вы расставите точки по центру каждой грани куба и затем соедините точки, образующие пространственные углы, получится новый многогранник внутри куба: октаэдр. И наоборот, если вы расставите точки по центру каждой грани октаэдра и соедините их между собой, получится куб. Та же дуальность связывает икосаэдр и додекаэдр.
Читать дальшеИнтервал:
Закладка:










