Эдвард Шейнерман - Путеводитель для влюбленных в математику

Вы можете проверить эти вычисления на калькуляторе за несколько секунд! Сложите все целые числа от 1 до 10, и вы получите 55.

Джеймс Стирлинг – шотландский математик X VIII века.

Скажем, в числе 0,053 первая значащая цифра 5. Когда мы говорим о первой значащей цифре, то подразумеваем первую цифру, отличную от нуля.

Если измерять рост в футах, почти все результаты будут начинаться с цифр 4, 5 или 6.

Я черпаю данные из «Справочника ЦРУ по странам мира». Он доступен в Сети по адресу https://www.cia.gov/library/publications/the-world-factbook.

Согласно актуальной версии справочника ЦРУ, в Китайской Народной Республике 1 379 302 771 граждан, в Республике Индия 1 281 935 911, в Республике Науру 9642 (все данные проверены в июле 2017). Наименьшее в мире количество граждан у Ватикана: 1000 человек (проверено в 2017 году). – Прим. пер.

Фрэнк Бенфорд (1883–1948) – американский инженер и физик, бо́льшую часть жизни работал в General Electric. – Прим. пер.

Саймон Ньюком (1835–1909) – американский астроном, математик и экономист. Работал в Морской академии в Вашингтоне и Военно-морской обсерватории США. Двоюродный прапрадед физика Уильяма Ньюкома (о парадоксе, названном его именем, пойдет речь в главе 23). – Прим. пер.

Мы приводим округленные значения. На самом деле ожидаемая частотность для 1 составляет 30,102999566398114…%. Скоро мы растолкуем, откуда берется это значение.

Обычно таблица умножения включает 10 строк и 10 столбцов, но умножение на 10 в нашем случае ничем не отличается от умножения на 1, поэтому один столбец мы выпускаем.

Можно наглядно увидеть трехмерную таблицу умножения на примере кубика Рубика. Некоторые варианты (например, 4 × 7 × 3 = 84) будут скрыты внутри кубика.

В десятимерной таблице умножения 9 10произведений, то есть чуть меньше 3,5 миллиарда чисел.

От лат. mantissa – «прибавка». – Прим. пер.

Например, мантисса числа 0,0043 равна 4,3, потому что 0,0043 = 4,3 × 10 –3.

Для читателей из стран, где стандартная единица измерения – метр, отмечу, что ярд немного меньше метра, а фут равен одной трети ярда.

Помните, что f (3) равно доле величин, мантисса которых меньше 3, а именно 1 или 2. Поэтому мы вычитаем долю измерений, начинающихся на 1.

Величина f (9) равна доле величин, мантисса которых меньше 9. Поэтому мы вычитаем долю величин, начинающихся на 1, 2, 3, 4 и 5.

Если мы переведем ярды в футы, то b = 3. Для других величин это число другое.

Нас ждет прокол, если ab >10 или ab < 1. Эта проблема поддается разрешению, но пока мы просто будем рассматривать только варианты, при которых 1 ≤ ab ≤ 10.

Этот раздел должен освежить ваши знания о десятичных логарифмах. Если вы знакомы с темой, можете листать дальше.

В оригинале десятичный логарифм обозначен log в соответствии с американской традицией пропускать нижний индекс «10», когда речь идет о десятичном логарифме. В русскоязычной литературе используется обозначение lg( x ). – Прим. пер.

Возьмите калькулятор, посчитайте обе величины и убедитесь, что я не ошибся.

Слово алгоритм происходит от имени персидского математика Аль-Хорезми (IX в. н. э.).

Даже эту операцию можно разбить на еще более элементарные. Например, нужно решить, чью тетрадь положить первой – Алисы или Алекса. Я сравниваю первые буквы. Они совпадают. Тогда я сравниваю вторые буквы – они снова совпадают. Третья буква в имени Алисы – «и», третья буква в имени Алекса – «е». Следовательно, тетрадка Алекса должна идти первой.

Если мы вычислим среднестатистическое количество операций, то получим средний случай.

Описанную процедуру называют сортировкой пузырьковым методом . Диаграмма иллюстрирует один раунд алгоритма.

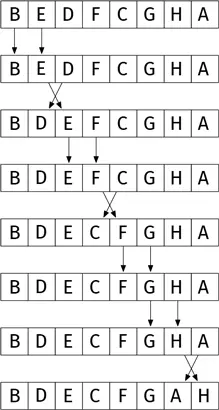
Обратите внимание: тетрадь A сместилась всего на одну позицию. Нам потребуется еще шесть раундов, чтобы она поднялась наверх.

Описанный метод называют сортировкой слиянием . Это хороший пример принципа «разделяй и властвуй»: сложная задача разбивается на несколько задач попроще, а затем решения объединяются.

Чарльз Понци – итальянский мошенник, создатель финансовой пирамиды в Бостоне в 1920 году. – Прим. пер.

Заметим, что пример не так прост, как кажется: первый раз слово «оскудение» обозначает состояние, а второй раз – процесс. – Прим. науч. ред.

Описание будет еще более точным, если мы формализуем процедуру соединения подмножеств, описанную выше.

Несколько простых примеров: НОД (10, 15) = 5; НОД (12, 16) = 4; НОД (13, 11) = 1; НОД (10, 20) = 10; НОД (17, 17) = 17.

Разложение на множители при поиске НОД ( a, b ) гораздо эффективнее, чем поиск делителей вплоть до меньшего из двух чисел a и b . Поиск простых множителей числа a потребует самое большее 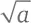операций деления. Это значительное усовершенствование первоначального алгоритма, но в случае стозначных чисел даже наш новый метод становится уже чертовский сложной задачей.

Например, если a = 100 и b = 40, частное q = 2 и остаток c = 20. Иными словами, 100 – 2 × 40 = 20.

10 693 = 4 × 2220 + 1813.

2220 = 1 × 1813 + 407.

1813 = 4 × 407 + 185.

407 = 2 × 185 + 37.

В главе 6 мы познакомились с концепцией взаимно простых чисел. Вот альтернативное определение: число a взаимно простое с b , если НОД ( a, b ) = 1. Так как алгоритм Евклида позволяет эффективно вычислить НОД двух чисел, он также позволяет выяснить, являются ли два числа взаимно простыми.

Данный метод неэффективен, однако не безнадежен. Мы знаем, что 364 × 286 кратно тому и другому числу. Будем надеяться на то, что набредем на общее кратное поменьше.

Мы выведем эту формулу площади треугольника на основании того, что площадь прямоугольника со сторонами a и b равна a × b .

Вот другой способ вычислить площадь данного треугольника. Он расположен внутри прямоугольника площадью 8 × 12 = 96. Необходимо вычесть из того числа площади трех «лишних» прямоугольных треугольников. Посчитать их несложно. Площадь треугольника слева 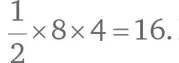Площадь верхнего треугольника справа 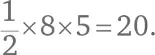Площадь нижнего треугольника справа равна 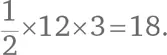Общая площадь «лишних» треугольников 18 + 20 + 16 = 54. Вычитаем это число из площади прямоугольника и получаем искомую площадь нашего треугольника: 96 – 54 = 42.